
 的垂线PA、QB,垂足分别为A、B,记λ=|AP|•|BQ|.
的垂线PA、QB,垂足分别为A、B,记λ=|AP|•|BQ|.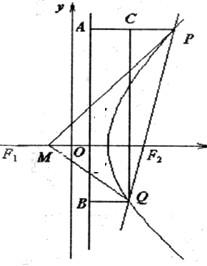 (Ⅰ)解:由|PF1|-|PF2|=2<|F1F2|知,点P的轨迹S是以F1、F2为焦点的双曲线右支.…(1分)
(Ⅰ)解:由|PF1|-|PF2|=2<|F1F2|知,点P的轨迹S是以F1、F2为焦点的双曲线右支.…(1分)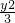 =1 (x≥1)…(5分)
=1 (x≥1)…(5分)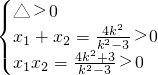 解得k2>3.…(9分)
解得k2>3.…(9分)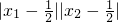 =
= (2x1-1)(2x2-1)=
(2x1-1)(2x2-1)= [4x1x2-2(x1+x2)+1]=x1x2-
[4x1x2-2(x1+x2)+1]=x1x2- +
+ …(11分)
…(11分)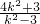 -
- +
+ =
= +
+ =
= +
+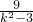 >
> . …(12分)
. …(12分) ,∴λ的最小值为
,∴λ的最小值为 .…(13分)
.…(13分) ||MF2|•|PQ|=9.…(14分)
||MF2|•|PQ|=9.…(14分) ,从而可求△PMQ的面积.
,从而可求△PMQ的面积.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| MP |
| MQ |
| 1 |
| 2 |
| |PA|+|QB| |
| |AB| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com