
| 组别 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 2 | 4 | 11 | 16 | 13 | 4 |
分析 (Ⅰ)根据题意,由频率分布表可得高度不低于80厘米的频数,进而由等可能事件的概率公式,计算可得答案;
(Ⅱ)设[40,50)组中的树苗为A、B,[90,100]组中的树苗为C、D、E、F用列表法可得移出1棵树苗的基本事件的数目与A、C同时被移出的事件数目,有等可能事件的概率公式计算可得答案.
解答 解:(Ⅰ)高度在80厘米以上共17棵,
高度在80厘米以上的概率p=$\frac{17}{50}$,
$\frac{90+220+65×11+75×16+85×13+95×4}{50}$=74.2;
(Ⅱ)事件“从[40,50)中移出1棵树苗,事件从[90,100]中移出2棵树苗,”
包含的基本事件是${C}_{2}^{1}$${C}_{4}^{2}$=12个,其中满足在[40,50)中和[90,100]中的树苗同时被移出的事件共2个
∴其概率p2=$\frac{1}{6}$.
点评 本题考查频率分布表的应用,涉及等可能事件的概率的计算,注意从频率分布表中分析出要求的数据及信息.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
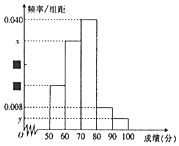 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a |  |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) |  | 0.08 |
| 第5组 | [90,100) | 2 | b |
| 合计 |  |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<4} | B. | {1,2,3} | C. | {0,1,2,3} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com