
【题目】如图,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)详见解析(2)![]()
【解析】
(1)推导出![]() ,
,![]() ,从而
,从而 ![]() 平面
平面![]() ,进而
,进而![]() ,再求出
,再求出![]() ,从而
,从而![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() ;
;
(2)解1:设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,
由![]() ,能求出点
,能求出点![]() 到平面
到平面![]() 的距离。
的距离。
解2:建立空间直角坐标系,利用空间中点到平面的距离公式计算可得。
(1)证明:∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,同理
,同理![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ;又四边形
;又四边形![]() 为菱形,∴
为菱形,∴![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)解1:设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,由(1)可知四边形
,由(1)可知四边形![]() 时直角梯形,
时直角梯形,![]() .又∵
.又∵![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,由
,由![]() ,解得:
,解得:![]() .
.
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解2:由(1)平面![]() 平面
平面![]() ,又平面
,又平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() 点,则
点,则![]() 平面
平面![]() ,所以
,所以![]() 即为点
即为点![]() 到平面
到平面![]() 的距离,分别以
的距离,分别以![]() ,
,![]() 为
为![]() ,
,![]() 轴建立直角坐标系,则
轴建立直角坐标系,则![]() ,
,![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某厂生产一种机器的固定成本为0.5万元,但每生产100台,需要加可变成本(即另增加投入)0.25万元,市场对此产品的年求量为500台,销售的收入函数为![]() (万元)(
(万元)(![]() ),其中
),其中![]() 是产品售出的数量(单位:百台).
是产品售出的数量(单位:百台).
(1)把利润表示为年产量的函数;
(2)年产量是多少时,工厂所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
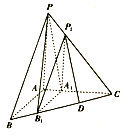
【题目】如图,在三棱锥![]() 中,
中,![]() 两两垂直,
两两垂直,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 与棱
与棱![]() 分别交于
分别交于![]() 三点.
三点.
(1)过![]() 作直线
作直线![]() ,使得
,使得![]() ,
,![]() ,请写出作法并加以证明;
,请写出作法并加以证明;
(2)若α将三梭锥P﹣ABC分成体积之比为8:19的两部分(其中,四面体P1A1B1C的体积更小),D为线段B1tC的中点,求直线P1D与平面PA1B1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代名词“刍童”原来是草堆的意思,关于“刍童”体积计算的描述,《九章算术》注曰:“倍上袤,下袤从之,亦倍下袤,上袤从之,各以其广乘之,并,以高乘之,皆六而一.”其计算方法是:将上底面的长乘二,与下底面的长相加,再与上底面的宽相乘,将下底面的长乘二,与上底面的长相加,再与下底面的宽相乘;把这两个数值相加,与高相乘,再取其六分之一.已知一个“刍童”的下底面是周长为18的矩形,上底面矩形的长为3,宽为2,“刍童”的高为3,则该“刍童”的体积的最大值为
A. ![]() B.
B. ![]() C. 39 D.
C. 39 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数 ,下列判断正确的是( )
,下列判断正确的是( )
A. ![]() 有最大值和最小值
有最大值和最小值
B. ![]() 的图象的对称中心为
的图象的对称中心为![]() (
(![]() )
)
C. ![]() 在
在![]() 上存在单调递减区间
上存在单调递减区间
D. ![]() 的图象可由
的图象可由![]() 的图象向左平移
的图象向左平移![]() 个单位而得
个单位而得
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量指数.空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.一环保人士记录去年某地某月10天的AQI的茎叶图如图.利用该样本估计该地本月空气质量优良(![]() )的天数(按这个月总共30天计算)为________.
)的天数(按这个月总共30天计算)为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连续掷3枚硬币,观察落地后这3枚硬币出现正面还是反面.(与先后顺序有关)
(1)写出这个试验的样本空间及样本点的个数;
(2)写出事件“恰有两枚正面向上”的集合表示.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com