
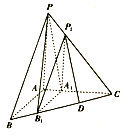
【题目】如图,在三棱锥![]() 中,
中,![]() 两两垂直,
两两垂直,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 与棱
与棱![]() 分别交于
分别交于![]() 三点.
三点.
(1)过![]() 作直线
作直线![]() ,使得
,使得![]() ,
,![]() ,请写出作法并加以证明;
,请写出作法并加以证明;
(2)若α将三梭锥P﹣ABC分成体积之比为8:19的两部分(其中,四面体P1A1B1C的体积更小),D为线段B1tC的中点,求直线P1D与平面PA1B1所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】分析:(1)取BC的中点H,连结AH,则直线AH即为要求的直线l;
(2)根据体积比得出P1A1=A1B1=2,将四棱锥分解成两个小三棱锥计算体积.
详解:(1)作法:取![]() 的中点
的中点![]() ,连接
,连接![]() ,则直线
,则直线![]() 即为要求作的直线
即为要求作的直线![]() .
.
证明如下:∵![]() ,
,![]() ,且
,且![]() ,∴
,∴![]() 平面
平面![]() .
.
∵平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,
,![]() 为
为![]() 的中点,则
的中点,则![]() ,从而直线
,从而直线![]() 即为要求作的直线
即为要求作的直线![]() .
.
(2)∵![]() 将三棱锥
将三棱锥![]() 分成体积之比为
分成体积之比为![]() 的两部分,
的两部分,
∴四面体![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积之比为
的体积之比为![]() ,
,
又平面![]() 平面
平面![]() ,∴
,∴![]() .
.
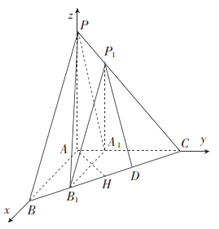
以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,设
,设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则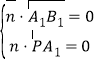 ,即
,即![]() ,
,
令![]() ,得
,得![]() .
.
则![]() .
.
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】独立性检验中,假设![]() :运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得
:运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得![]() 的观测值
的观测值![]() .下列结论正确的是
.下列结论正确的是

A. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动有关
B. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动无关
C. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动有关
D. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
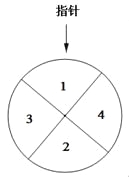
①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个;
,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() 且
且![]() )在区间
)在区间![]() 上的最大值与最小值之和为
上的最大值与最小值之和为![]() ,
,![]() ,其中
,其中![]() .
.
(1)直接写出![]() 的解析式和单调性;
的解析式和单调性;
(2)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若
,若![]() ,使得对
,使得对![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,错误的是( )
A. 一条直线与两个平行平面中的一个相交,则必与另一个平面相交
B. 平行于同一平面的两条直线不一定平行
C. 如果平面![]() 垂直,则过
垂直,则过![]() 内一点有无数条直线与
内一点有无数条直线与![]() 垂直.
垂直.
D. 如果平面![]() 不垂直于平面
不垂直于平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com