
【题目】已知数列![]() 的前项和为
的前项和为![]() ,且
,且![]() ,记
,记![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由![]() ,得
,得![]() ,两式
,两式
相减得![]() ,即
,即![]() ,经验证
,经验证![]() 时也成立;(2)
时也成立;(2)![]() ,利用裂项相消法求和即可得结果.
,利用裂项相消法求和即可得结果.
试题解析:(1)当![]() 时,
时, ![]() ,则
,则![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
相减得![]() ,即
,即![]() ,经验证
,经验证![]() 时也成立,
时也成立,
所以数列![]() 的通项公式为
的通项公式为![]() .
.
(2)![]() ,
,
所以数列![]() 的前
的前![]() 项和为:
项和为:
![]()
![]() .
.
【方法点晴】本题主要考查等差数列的通项与求和公式之间的关系,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:
(1) ![]() ;(2)
;(2) ![]()
![]() ;
;
(3)![]() ;(4)
;(4)![]()
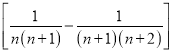 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.


科目:高中数学 来源: 题型:
【题目】某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:
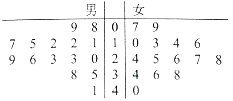
若将月均课外阅读时间不低于30小时的学生称为“读书迷”.
(1)将频率视为概率,估计该校900名学生中“读书迷”有多少人?
(2)从已抽取的7名“读书迷”中随机抽取男、女“读书迷”各1人,参加读书日宣传活动.
(i)共有多少种不同的抽取方法?
(ii)求抽取的男、女两位“读书迷”月均读书时间相差不超过2小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=1,an+an+1=( ![]() )n , Sn=a1+4a2+42a3+…+4n﹣1an , 类比课本中推导等比数列前项和公式的方法,可求得5Sn﹣4nan= .
)n , Sn=a1+4a2+42a3+…+4n﹣1an , 类比课本中推导等比数列前项和公式的方法,可求得5Sn﹣4nan= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市2017年3月1日至16日的空气质量指数趋势图,空气质量指数![]() 小于
小于![]() 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于![]() 表示空气重度污染.
表示空气重度污染.
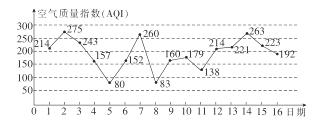
(1)若该人随机选择3月1日至3月14日中的某一天到达该市,到达后停留![]() 天(到达当日算
天(到达当日算![]() 天),求此人停留期间空气重度污染的天数为
天),求此人停留期间空气重度污染的天数为![]() 天的概率;
天的概率;
(2)若该人随机选择3月7日至3月12日中的![]() 天到达该市,求这
天到达该市,求这![]() 天中空气质量恰有
天中空气质量恰有![]() 天是重度污染的概率.
天是重度污染的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3sin(2x+ ![]() )的图象为C,关于函数f(x)及其图象的判断如下: ①图象C关于点(
)的图象为C,关于函数f(x)及其图象的判断如下: ①图象C关于点( ![]() ,0)对称;
,0)对称;
②图象C关于直线x= ![]() 对称;
对称;
③由图象C向右平移 ![]() 个单位长度可以得到y=3sin2x的图象;
个单位长度可以得到y=3sin2x的图象;
④函数f(x)在区间(﹣ ![]() ,
, ![]() )内是减函数;
)内是减函数;
⑤函数|f(x)+1|的最小正周期为 ![]() .
.
其中正确的结论序号是 . (把你认为正确的结论序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com