
分析 (Ⅰ)直接由曲线C的极坐标方程求出曲线C的直角坐标方程即可;
(Ⅱ)把直线l的参数方程代入曲线C的方程得5t2+4t-12=0,求出t1+t2和t1t2的值,由此能求出|AB|.
解答 解:(Ⅰ)∵曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12,
∴曲线C的直角坐标方程为3x2+4y2=12,化简得$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)把直线l的参数方程$\left\{{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$代入曲线C的方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,化简整理得5t2+4t-12=0,
∴${t}_{1}+{t}_{2}=-\frac{4}{5}$,${t}_{1}{t}_{2}=-\frac{12}{5}$,
∴|AB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}=\sqrt{\frac{256}{25}}=\frac{16}{5}$.
点评 本题考查直线的极坐标方程、曲线的直角坐标方程的求法,考查弦长的求法,考查直角坐标方程、极坐标方程、参数方程的互化,是基础题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
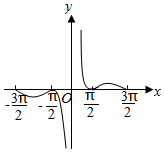 已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )| A. | $\frac{|cos3x|}{x}$ | B. | $\frac{1+cos2x}{2x}$ | ||
| C. | $\frac{(4{x}^{2}-{π}^{2})(4{x}^{2}-9{π}^{2})}{{x}^{5}}$ | D. | $\frac{|sin2x|}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,$\frac{1}{3}$] | B. | [-$\frac{1}{2}$,$\frac{1}{3}$] | C. | [-$\frac{1}{2}$,1) | D. | [-$\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com