
分析 (1)利用函数奇偶性的定义判断f(-x)与f(x)的关系,在定义域关于原点对称的前提下,相等为偶函数,相反为奇函数;
(2)利用导数与函数单调性的关系,对函数求导,通过导数的符号判断函数的单调性;
(3)利用基本不等式以及函数的单调性求最值.
解答 解:(1)函数f(x)的定义域为{x|x≠0,x∈R}关于原点对称
因为f(-x)=-x-$\frac{4}{x}$=-f(x).
所以f(x)是奇函数.
(2)证明:f'(x)=1-$\frac{4}{{x}^{2}}$,f'(x)在区间(0,2],f'(x)<0,所以在[0,2]是单调减函数,在区间[2,+∞)上f'(x)>0,所以f(x)在[2,+∞)是单调增函数;
(3)当x∈(0,+∞)时,f(x)≥2$\sqrt{x•\frac{4}{x}}$=4,当且仅当x=2时f(x)取最小值4,无最大值.
点评 本题主要考查函数的单调性和奇偶性的判断与证明,同时还考查了利用性质作出函数图象,这类作图不是很准确,但在数形结合中解决问题很有效


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
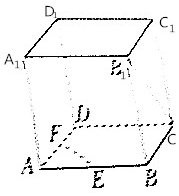 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
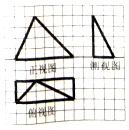 我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理:“幂势既同,则积不容异”.“势”即是高,“幂”即是面积.意思是说如果两等高的几何体在同高处截得两几何体的截面积相等,那么这两个几何体的体积相等.已知某不规则几何体与如图所对应的几何体满足:“幂势同”,则该不规则几何体的体积为(图中的网格纸中的小正方形的边长为1)( )
我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理:“幂势既同,则积不容异”.“势”即是高,“幂”即是面积.意思是说如果两等高的几何体在同高处截得两几何体的截面积相等,那么这两个几何体的体积相等.已知某不规则几何体与如图所对应的几何体满足:“幂势同”,则该不规则几何体的体积为(图中的网格纸中的小正方形的边长为1)( )| A. | 4 | B. | 8 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(\frac{1}{2})<f(-\frac{3}{2})<f(3)$ | B. | $f(3)<f(-\frac{3}{2})<f(\frac{1}{2})$ | C. | $f(\frac{1}{2})<f(3)<f(-\frac{3}{2})$ | D. | $f(3)<f(\frac{1}{2})<f(-\frac{3}{2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com