
| A. | -$\frac{1}{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{2\sqrt{3}}{3}$ |
分析 作出M在准线上的射影,根据|KM|:|MD|确定|KD|:|KM|的值,进而列方程求得m,再求出M的坐标
解答 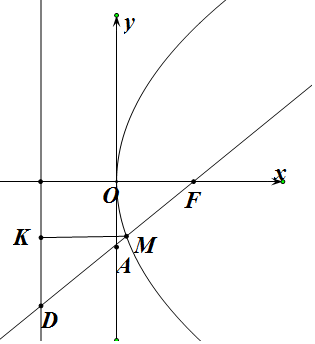 解:依题意F点的坐标为($\frac{m}{4}$,0),
解:依题意F点的坐标为($\frac{m}{4}$,0),
设M在准线上的射影为K,
由抛物线的定义知|MF|=|MK|,
∵|FM|:|MD|=1:2:
则|KD|:|KM|=$\sqrt{3}$:1,
kFD=$\sqrt{3}$,
kFD=$\frac{0+\sqrt{3}}{\frac{m}{4}-0}$=$\frac{4\sqrt{3}}{m}$
∴$\frac{4\sqrt{3}}{m}$=$\sqrt{3}$,求得m=4
∴直线FM的方程为y=$\sqrt{3}$(x-1),
与y2=4x,联立方程组,解得x=3(舍去)或x=$\frac{1}{3}$,
∴y2=$\frac{4}{3}$,
解y=-$\frac{2\sqrt{3}}{3}$或y=$\frac{2\sqrt{3}}{3}$(舍去),
故M的坐标为($\frac{1}{3}$,-$\frac{2\sqrt{3}}{3}$),
故选:D
点评 本题主要考查了抛物线的简单性质.抛物线中涉及焦半径的问题常利用抛物线的定义转化为点到准线的距离来解决.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{n}$ | B. | $\frac{n}{n+1}$ | C. | $\frac{1}{n+1}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
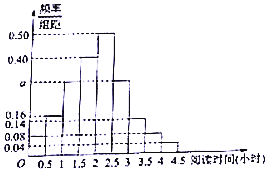 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成样本的频率分布直方图如图所示.
某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成样本的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com