
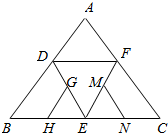
 如图是正四面体的平面展开图,G、H、M、N分别为DE、BE、EF、EC的中点,在这个正四面体中,
如图是正四面体的平面展开图,G、H、M、N分别为DE、BE、EF、EC的中点,在这个正四面体中,分析 正四面体的平面展开图复原为正四面体A(B、C)-DEF,
①,依题意,GH∥AD,而AD与EF异面,从而可判断GH与EF不平行;
②,假设BD与MN共面,可得A、D、E、F四点共面,导出矛盾,从而可否定假设,肯定BD与MN为异面直线;
③,依题意知,GH∥AD,MN∥AF,∠DAF=60°,于是可判断GH与MN成60°角;
④,连接GF,那么A点在平面DEF的射影肯定在GF上,通过线面垂直得到线线垂直.
解答 解:将正四面体的平面展开图复原为正四面体A(B、C)-DEF,如图: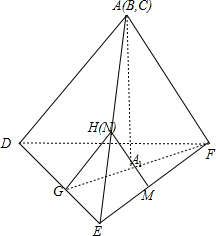
对于①,G、H分别为DE、BE的中点,则GH∥AD,而AD与EF异面,故GH与EF不平行,故①错误;
对于②,BD与MN为异面直线,正确(假设BD与MN共面,则A、D、E、F四点共面,与ADEF为正四面体矛盾,故假设不成立,故BD与MN异面);
对于③,依题意,GH∥AD,MN∥AF,∠DAF=60°,故GH与MN成60°角,故③正确;
对于④,连接GF,A点在平面DEF的射影A1在GF上,∴DE⊥平面AGF,DE⊥AF,
而AF∥MN,∴DE与MN垂直,故④正确.
综上所述,正确命题的序号是②③④,
故答案为:②③④.
点评 本题考查命题的真假判断与应用,着重考查空间直线间的位置关系,突出考查异面直线的判定、两直线所成的角的概念及应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 浑南“万达广场”五一期间举办“万达杯”游戏大赛.每5人组成一队,编号为1,2,3,4,5,在其中的投掷飞镖比赛中,要求随机抽取3名队员参加,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面为圆形,ABCD为正方形).每队至少有2人“成功”则可获得奖品(其中任何两位队员“成功”与否互不影响).
浑南“万达广场”五一期间举办“万达杯”游戏大赛.每5人组成一队,编号为1,2,3,4,5,在其中的投掷飞镖比赛中,要求随机抽取3名队员参加,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面为圆形,ABCD为正方形).每队至少有2人“成功”则可获得奖品(其中任何两位队员“成功”与否互不影响).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DO与AB所成角的余弦值等于$\frac{\sqrt{6}}{6}$.
如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DO与AB所成角的余弦值等于$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x<1或x>3 | B. | x<-3或x>-1 | ||
| C. | x<-3或-1<x<1或x>3 | D. | 0≤x<1或x>3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x∈(-∞,-2)∪[2,+∞) | B. | x∈(-∞,-2]∪[2,+∞) | C. | x∈(-2,2) | D. | x∈[-2,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com