
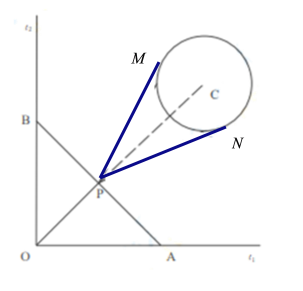
【题目】如图,在一旅游区内原有两条互相垂直且相交于点O的道路l1,l2,一自然景观的边界近似为圆形,其半径约为1千米,景观的中心C到l1,l2的距离相等,点C到点O的距离约为10千米.现拟新建四条游览道路方便游客参观,具体方案:在线段OC上取一点P,新建一条道路OP,并过点P新建两条与圆C相切的道路PM,PN(M,N为切点),同时过点P新建一条与OP垂直的道路AB(A,B分别在l1,l2上).为促进沿途旅游经济,新建道路长度之和越大越好,求新建道路长度之和的最大值.(所有道路宽度忽略不计)
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 的侧棱和底面边长相等,在这个正四棱锥的
的侧棱和底面边长相等,在这个正四棱锥的![]() 条棱中任取两条,按下列方式定义随机变量
条棱中任取两条,按下列方式定义随机变量![]() 的值:
的值:
若这两条棱所在的直线相交,则![]() 的值是这两条棱所在直线的夹角大小(弧度制);
的值是这两条棱所在直线的夹角大小(弧度制);
若这两条棱所在的直线平行,则![]() ;
;
若这两条棱所在的直线异面,则![]() 的值是这两条棱所在直线所成角的大小(弧度制).
的值是这两条棱所在直线所成角的大小(弧度制).
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,左焦点为
,左焦点为![]() ,右顶点为
,右顶点为![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,若直线
两点,若直线![]() 垂直于
垂直于![]() 轴时,有
轴时,有![]() .
.
(1)求椭圆的方程;
(2)设直线![]() :
: ![]() 上两点
上两点![]() ,
, ![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与椭圆相交于点
与椭圆相交于点![]() (
(![]() 异于点
异于点![]() ),直线
),直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2019年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示:
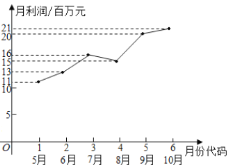
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年4月份的利润;
的线性回归方程,并预测该公司2020年4月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有A,B两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料的使用寿命不同,现对A,B两种型号的新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:

经甲公司测算平均每件新型材料每月可以带来6万元收人入,不考虑除采购成本之外的其他成本,A型号材料每件的采购成本为10万元,B型号材料每件的采购成本为12万元.假设每件新型材料的使用寿命都是整月数,且以频率作为每件新型材料使用寿命的概率,如果你是甲公司的负责人,以每件新型材料产生利润的平均值为决策依据,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程![]() ,其中
,其中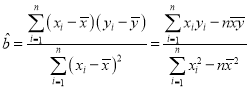 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月25日-27日,北京召开第二届“一带一路”国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬新时代的中国女排精神.甲、乙两个女排校队举行一场友谊比赛,采用五局三胜制(即某队先赢三局则获胜,比赛随即结束).若两队的竞技水平和比赛状态相当,且每局比赛相互独立,则比赛结束时已经进行的比赛局数的数学期望是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某地区气象水文部门长期统计,可知该地区每年夏季有小洪水的概率为0.25,有大洪水的概率为0.05.
(1)从该地区抽取的![]() 年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,求
年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,求![]() 的值;
的值;
(2)今年夏季该地区某工地有许多大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失20000元.为保护设备,有以下3种方案:
方案1:修建保护围墙,建设费为3000元,但围墙只能防小洪水.
方案2:修建保护大坝,建设费为7000元,能够防大洪水.
方案3:不采取措施.
试比较哪一种方案好,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com