练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．若数列{an}满足a1=1，an+1=an+2（n∈N*），则a4等于（　　）
    A．7B．9C．11D．13

    分析 由已知可得数列{an}是公差为2的等差数列，再由等差数列的通项公式得答案．

    解答 解：由an+1=an+2，得an+1-an=2，
    ∴数列{an}是公差为2的等差数列，
    又a1=1，
    ∴a4=a1+3d=1+3×2=7．
    故选：A．

    点评 本题考查等差数列的通项公式，是基础的计算题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．已知等差数列{an}的前n项和为Sn，且a3=3，S7=28，在等比数列{bn}中，b3=4，b4=8．
    （1）求an及bn；
    （2）设数列{anbn}的前n项和为Tn，求Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．甲、乙两人约好一同去看《变形金刚5》，两人买完了电影票后，偶遇丙也来看这场电影，此时还剩9张该场电影的电影票，电影票的座位信息如表．
    1排4号1排5号1排8号
    2排4号
    3排1号3排5号
    4排1号4排2号4排8号
    丙从这9张电影票中挑选了一张，甲、乙询问丙所选的电影票的座位信息．丙只将排数告诉了甲，只将号数告诉了乙．下面是甲、乙关于丙所选电影票的具体座位信息的一段对话：
    甲对乙说：“我不能确定丙的座位信息，你肯定也不能确定．”
    乙对甲说：“本来我不能确定，但是现在我能确定了．”
    甲对乙说：“哦，那我也能确定了！”
    根据上面甲、乙的对话，判断丙选择的电影票是（　　）
    A．4排8号B．3排1号C．2排4号D．1排5号

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．观察下列不等式：
    （1）1≤sin2α+cos2α≤1
    （2）$\frac{1}{2}$≤sin4α+cos4α≤1
    （3）$\frac{1}{4}$≤sin6α+cos6α≤1
    …
    由此规律推测，第n个不等式为：$\frac{1}{{2}^{n-1}}$≤sin2nα+cos2nα≤1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

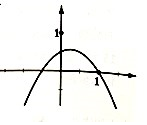
    2．如图是函数f（x）=-x2+ax+b的部分图象，f′（x）是f（x）的导函数，则函数g（x）=ex-f′（x）的零点所在的区间是（　　）
    A．（-1，-$\frac{1}{2}$）B．（-$\frac{1}{2}$，0）C．（0，$\frac{1}{2}$）D．（$\frac{1}{2}$，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知一次函数f（x）=ax-2．
    （1）当a=3时，解不等式|f（x）|＜4；
    （2）若不等式|f（x）|≤3对任意x∈[0，1]恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．某市为提升城市品位，开展植树造林，创建国家森林城市，为了保证树苗的质量，林管部门要在植树前对树苗高度进行抽测，现抽测了6株某种树苗的高度（单位：厘米），得到如图1茎叶图．
    （1）求这6株树苗高度的中位数和平均数$\overline{x}$；
    （2）若将这6株树苗的高度依次输入如图2程序框图．求输出δ的值．（要有解答过程）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知向量$\overrightarrow{AB}$，$\overrightarrow{AC}$，$\overrightarrow{AD}$在正方形网格中的位置如图所示，若$\overrightarrow{AC}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$，则λμ=（　　）
    A．-3B．3C．-4D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．同时具有性质：①图象的一个零点和其相邻对称轴间的距离是$\frac{π}{4}$；②在区间[-$\frac{π}{6}$，$\frac{π}{3}$]上是增函数的一个函数为（　　）
    A．y=cos（$\frac{x}{2}$+$\frac{π}{6}$）B．y=sin（$\frac{x}{2}$+$\frac{π}{6}$）C．y=sin（2x-$\frac{π}{6}$）D．y=cos（2x-$\frac{π}{6}$）

    查看答案和解析>>

    同步练习册答案