
【题目】已知焦点在x轴上,中心在坐标原点的椭圆C的离心率为 ![]() ,且过点(
,且过点( ![]() ,1). (Ⅰ)求椭圆C的方程;
,1). (Ⅰ)求椭圆C的方程;
(Ⅱ)直线l分别切椭圆C与圆M:x2+y2=R2(其中3<R<5)于A、B两点,求|AB|的最大值.
【答案】解:(Ⅰ)设椭圆的方程为 ![]() ,则
,则 ![]() ,
, ![]() a, ∴
a, ∴ ![]() ,
,
∵椭圆过点 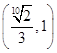 ,∴
,∴ 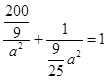 ,解得 a2=25,b2=9,
,解得 a2=25,b2=9,
故椭圆C的方程为 ![]()
(Ⅱ)设A(x1 , y1),B(x2 , y2)分别为直线l与椭圆和圆的切点,
直线AB的方程为y=kx+m,因为A既在椭圆上,又在直线AB上,
从而有 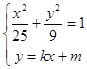 ,消去y得:(25k2+9)x2+50kmx+25(m2﹣9)=0,
,消去y得:(25k2+9)x2+50kmx+25(m2﹣9)=0,
由于直线与椭圆相切,
故△=(50kmx)2﹣4(25k2+9)×25(m2﹣9)=0,从而可得:m2=9+25k2 , ①,x1= ![]() ,②
,②
由 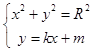 .消去y得:(k2+1)x2+2kmx+m2﹣R2=0,
.消去y得:(k2+1)x2+2kmx+m2﹣R2=0,
由于直线与圆相切,得m2=R2(1+k2),③,x2= ![]() ,④
,④
由②④得:x2﹣x1= ![]() ,由①③得:k2=
,由①③得:k2= ![]() ,
,
∴|AB|2=(x2﹣x1)2+(y2﹣y1)2=(1+k2)(x2﹣x1)2
= ![]() =
= 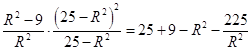
![]()
即|AB|≤2,当且仅当R= ![]() 时取等号,所以|AB|的最大值为2
时取等号,所以|AB|的最大值为2
【解析】(Ⅰ)设出椭圆的方程,根据离心率及椭圆过点( ![]() ,1)求出待定系数,即得椭圆的方程.(Ⅱ)用斜截式设出直线的方程,代入椭圆的方程,化为关于x的一元二次方程,利用根与系数的关系,化简|AB|的解析式并利用基本不等式求出其最大值.
,1)求出待定系数,即得椭圆的方程.(Ⅱ)用斜截式设出直线的方程,代入椭圆的方程,化为关于x的一元二次方程,利用根与系数的关系,化简|AB|的解析式并利用基本不等式求出其最大值.
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).


科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点,设异面直线EM与AF所成的角为θ,则cosθ的最大值为 . 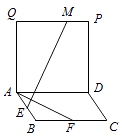
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是内角A,B,C的对边,AB=5,cos∠ABC= ![]() .
. 
(1)若BC=4,求△ABC的面积S△ABC;
(2)若D是边AC的中点,且BD= ![]() ,求边BC的长.
,求边BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元). (Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ax,g(x)=ex﹣3ax,其中a为实数,若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,则a的取值范围是( )
A.( ![]() ,+∞)
,+∞)
B.[ ![]() ,+∞)
,+∞)
C.(1,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=﹣x3+ax2+bx+c的导数f'(x)满足f'(﹣1)=0,f'(2)=9.
(1)求f(x)的单调区间;
(2)f(x)在区间[﹣2,2]上的最大值为20,求c的值.
(3)若函数f(x)的图象与x轴有三个交点,求c的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com