
分析 (1)设出等差数列的公差,由已知列式求得首项和公差,则{an}的通项公式可求;
(2)把{an}的通项公式代入${b_n}=\frac{a_n}{{{a_{n-1}}}}+\frac{{{a_{n-1}}}}{a_n}-2$,整理后利用裂项相消法求数列{bn}的前n项和Sn.
解答 解:(1)设等差数列{an}的公差为d,
由a1,a3,a7成等比数列,得$\left\{{\begin{array}{l}{2d=2}\\{{a_3}^2={a_1}•{a_7}}\end{array}}\right.$,即$\left\{{\begin{array}{l}{d=1}\\{{{({{a_1}+2d})}^2}={a_1}•({{a_1}+6d})}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{d=1}\\{{a_1}=2}\end{array}}\right.$.
∴an=n+1;
(2)由(1)可知,${b_n}=\frac{a_n}{{{a_{n-1}}}}+\frac{{{a_{n-1}}}}{a_n}-2$=$\frac{n+1}{n}+\frac{n}{n+1}-2$
=$\frac{(n+1)^{2}+{n}^{2}-2{n}^{2}-2n}{n(n+1)}=\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$.
∴${S_n}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n}-\frac{1}{n+1}=\frac{n}{n+1}$.
点评 本题考查等比数列的性质,考查等差数列通项公式的求法,训练了裂项相消法求数列的前n项和,是中档题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤-4 | B. | -4≤a≤6 | C. | a≤-4或a≥6 | D. | a≥6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 古文迷 | 非古文迷 | 合计 | |
| 男生 | 26 | 24 | 50 |
| 女生 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
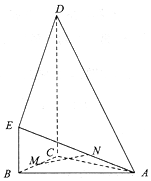 如图,多面体ABCDE中,AB=AC,平面BCDE⊥平面ABC,BE∥CD,CD⊥BC,BE=1,BC=2,CD=3,M为BC的中点.
如图,多面体ABCDE中,AB=AC,平面BCDE⊥平面ABC,BE∥CD,CD⊥BC,BE=1,BC=2,CD=3,M为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{2}{7},1})$ | B. | $({\frac{1}{3},3})$ | C. | $({\frac{1}{2},2})$ | D. | $({2,\frac{7}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 648个 | B. | 720个 | C. | 900个 | D. | 1000个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com