
分析 (Ⅰ)由$x+\frac{π}{4}≠kπ+\frac{π}{2}$,得$x≠kπ+\frac{π}{4}$,k∈Z,可得f(x)的定义域;
(Ⅱ)设β∈(0,π),且$f(β)=2cos(β-\frac{π}{4})$,整理得$sin(β+\frac{π}{4})•[2cos(β+\frac{π}{4})-1]=0$,即可求β的值.
解答 解:(Ⅰ)由$x+\frac{π}{4}≠kπ+\frac{π}{2}$,得$x≠kπ+\frac{π}{4}$,k∈Z.[(3分)]
所以 函数f(x)的定义域是$\{x|x≠kπ+\frac{π}{4},k∈{Z}\}$.[(4分)]
(Ⅱ)依题意,得$tan(β+\frac{π}{4})=2cos(β-\frac{π}{4})$.[(5分)]
所以$\frac{{sin(β+\frac{π}{4})}}{{cos(β+\frac{π}{4})}}=2sin(β+\frac{π}{4})$,[(7分)]
整理得$sin(β+\frac{π}{4})•[2cos(β+\frac{π}{4})-1]=0$,[(8分)]
所以$sin(β+\frac{π}{4})=0$,或$cos(β+\frac{π}{4})=\frac{1}{2}$.[(10分)]
因为 β∈(0,π),所以$β+\frac{π}{4}∈(\frac{π}{4}\;,\frac{5π}{4}\;)$,[(11分)]
由$sin(β+\frac{π}{4})=0$,得$β+\frac{π}{4}=π$,$β=\frac{3π}{4}$;[(12分)]
由$cos(β+\frac{π}{4})=\frac{1}{2}$,得$β+\frac{π}{4}=\frac{π}{3}$,$β=\frac{π}{12}$.
所以$β=\frac{π}{12}$,或$β=\frac{3π}{4}$.[(13分)]
点评 本题考查正切函数的定义域,考查特殊角三角函数值的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{2}$ | B. | $\sqrt{31}$ | C. | $\sqrt{33}$ | D. | $4\sqrt{2}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
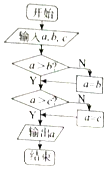 执行如图所示的程序框图,若输入三个数a=log36,b=log48,c=1.22,则输出的结果为( )
执行如图所示的程序框图,若输入三个数a=log36,b=log48,c=1.22,则输出的结果为( )| A. | log36 | B. | log48 | C. | 1.22 | D. | log23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=sinx | C. | $y=\frac{1}{{{x^2}+1}}$ | D. | $y=\sqrt{1-{x^2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|x≥-1} | C. | {x|0<x≤1} | D. | {x|-1≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com