
分析 (Ⅰ)根据相关数的定义判断即可;
(Ⅱ)根据相关数的定义得到m≤n+2时,m一定不是集合A2n的“相关数”,得到m≥n+3,从而证明结论;
(Ⅲ)根据m≥n+3,将集合A2n的元素分成n组,对A2n的任意一个含有n+3个元素的子集p,必有三组${C}_{{i}_{1}}$,${C}_{{i}_{2}}$,${C}_{{i}_{3}}$同属于集合P,不妨设${D}_{{j}_{4}}$与${C}_{{i}_{3}}$无相同元素,此时这4个元素之和为[i1+(2n+1-i1)+(2n-j4)]=4n+1,从而求出m的最小值.
解答 解:(Ⅰ)当n=3时,A6={1,2,3,4,5,6},4n+1=13,
①对于A6的含有5个元素的子集{2,3,4,5,6},
因为2+3+4+5>13,
所以5不是集合A6的“相关数”;
②A6的含有6个元素的子集只有{1,2,3,4,5,6},
因为1+3+4+5=13,
所以6是集合A6的“相关数”.
(Ⅱ)考察集合A2n的含有n+2个元素的子集B={n-1,n,n+1,…,2n},
B中任意4个元素之和一定不小于(n-1)+n+(n+1)+(n+2)=4n+2.
所以n+2一定不是集合A2n的“相关数”;
所以当m≤n+2时,m一定不是集合A2n的“相关数”,
因此若m为集合A2n的“相关数”,必有m≥n+3,
即若m为集合A2n的“相关数”,必有m-n-3≥0;
(Ⅲ)由(Ⅱ)得 m≥n+3,
先将集合A2n的元素分成如下n组:
Ci=(i,2n+1-i),(1≤n),
对A2n的任意一个含有n+3个元素的子集p,
必有三组${C}_{{i}_{1}}$,${C}_{{i}_{2}}$,${C}_{{i}_{3}}$同属于集合P,
再将集合A2n的元素剔除n和2n后,分成如下n-1组:
Dj=(j,2n-j),(1≤j≤n-1),
对于A2n的任意一个含有n+3个元素的子集P,必有一组${D}_{{j}_{4}}$属于集合P,
这一组${D}_{{j}_{4}}$与上述三组${C}_{{i}_{1}}$,${C}_{{i}_{2}}$,${C}_{{i}_{3}}$中至少一组无相同元素,
不妨设${D}_{{j}_{4}}$与${C}_{{i}_{3}}$无相同元素.
此时这4个元素之和为[i1+(2n+1-i1)+(2n-j4)]=4n+1,
所以集合A2n的“相关数”m的最小值为n+3.
点评 本题考查了相关数的定义及其应用,考查新定义的理解,是一道中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | e-1 | B. | 1-e | C. | $1-\frac{1}{e}$ | D. | $\frac{1}{e}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
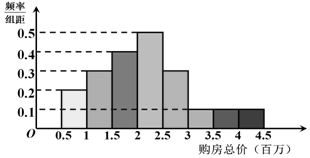
| 购房总价(万) | (0,200] | (200,400] | (400,+∞) |
| 税率 | 1% | 1.5% | 3% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x∈R|0<x<1} | B. | {x∈R|0<x<2} | C. | {x∈R|-1<x<0} | D. | {x∈R|-1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 总能分别作出正弦线、余弦线、正切线 | |
| B. | 总能分别作出正弦线、余弦线、正切线,但可能不只一条 | |
| C. | 正弦线、余弦线、正切线都可能不存在 | |
| D. | 正弦线、余弦线总存在,但正切线不一定存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com