
| 购房总价(万) | (0,200] | (200,400] | (400,+∞) |
| 税率 | 1% | 1.5% | 3% |
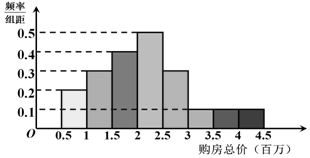
分析 (Ⅰ)由频率分布直方图求出购房总价在300万以上的频率,由此能估计该小区房子的总价在300万以上的房子的套数.
(Ⅱ)由频率分布直方图,能求出该小区购房者缴纳契税的平均值.
解答 (本小题满分12分)
解:(Ⅰ)由频率分布直方图可知,购房总价在300万以上的频率为:
0.1×0.5+0.1×0.5+0.1×0.5=0.15,(3分)
2000×0.15=300,
故估计该小区有300套房子的总价在300万以上.(4分)
(Ⅱ)由频率分布直方图,以及契税标准可知:
当购房总价是1百万时,契税为1万,频率为0.1;
当购房总价是1.5百万时,契税为1.5万,频率为0.15;
当购房总价是2百万时,契税为2万,频率为0.2;
当购房总价是2.5百万时,契税为3.75万,频率为0.25;
当购房总价是3百万时,契税为4.5万,频率为0.15;
当购房总价是3.5百万时,契税为5.25万,频率为0.05;
当购房总价是4百万时,契税为6万,频率为0.05;
当购房总价是4.5百万时,契税为13.5万,频率为0.05;(8分)
依题意可知该小区购房者缴纳契税的平均值为:
1×0.1+1.5×0.15+2×0.2+3.75×0.25+4.5×0.15+5.25×0.05+6×0.05+13.5×0.05=3.575,
故该小区购房者缴纳契税的平均值为3.575万元.(12分)
点评 本题考查频率分布直方图的性质及应用等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{121}{2}$,81] | B. | [$\frac{121}{2}$,73] | C. | [65,73] | D. | [65,81] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{2}$ | B. | $\sqrt{31}$ | C. | $\sqrt{33}$ | D. | $4\sqrt{2}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.4 | B. | 0.6 | C. | 0.7 | D. | 0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
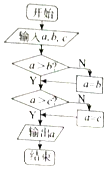 执行如图所示的程序框图,若输入三个数a=log36,b=log48,c=1.22,则输出的结果为( )
执行如图所示的程序框图,若输入三个数a=log36,b=log48,c=1.22,则输出的结果为( )| A. | log36 | B. | log48 | C. | 1.22 | D. | log23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com