
分析 (1)设设椭圆E的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,焦距为2c,根据题意列方程组求出a,b即可;
(2)联立方程组消元,令△>0求出m的范围,根据根与系数的关系和弦长公式得出MN,再计算原点到直线l的距离,得出三角形的面积关于m的函数,从而求得面积的最大值.
解答 解:(1)设椭圆E的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,焦距为2c,
由题意可知$\left\{\begin{array}{l}{b=c}\\{2a=2\sqrt{2}}\\{{a}^{2}-{b}^{2}={c}^{2}}\end{array}\right.$,解得a=$\sqrt{2}$,b=1,
∴椭圆E的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(2)联立方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=2x+m}\end{array}\right.$,消元得:9x2+8mx+2m2-2=0,
∵椭圆与直线交于M,N两点,
∴△=64m2-36(2m2-2)=72-8m2>0,
∴-3<m<3.
设M(x1,y1),N(x2,y2),则x1+x2=-$\frac{8m}{9}$,x1x2=$\frac{2{m}^{2}-2}{9}$,
∴MN=$\sqrt{5}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{5}$•$\sqrt{\frac{64{m}^{2}}{81}-\frac{8({m}^{2}-1)}{9}}$=$\frac{2\sqrt{10}}{9}$•$\sqrt{9-{m}^{2}}$,
又原点O到直线l的距离d=$\frac{|m|}{\sqrt{5}}$,
∴S△MON=$\frac{1}{2}$•MN•d=$\frac{1}{2}×$$\frac{2\sqrt{10}}{9}$•$\sqrt{9-{m}^{2}}$×$\frac{|m|}{\sqrt{5}}$=$\frac{\sqrt{2}•\sqrt{9-{m}^{2}}}{9}•|m|$=$\frac{\sqrt{2}}{9}•$$\sqrt{9{m}^{2}-{m}^{4}}$,
令f(m)=9m2-m4=-(m2-$\frac{9}{2}$)2+$\frac{81}{4}$,
∵-3<m<3,∴0≤m2<9,
∴当m2=$\frac{9}{2}$时,f(m)取得最大值$\frac{81}{4}$,
∴S△MON的最大值为$\frac{\sqrt{2}}{9}×\sqrt{\frac{81}{4}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了椭圆的性质,直线与椭圆的位置关系,注意弦长公式,根与系数关系的应用,属于中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
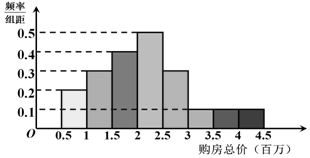
| 购房总价(万) | (0,200] | (200,400] | (400,+∞) |
| 税率 | 1% | 1.5% | 3% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 总能分别作出正弦线、余弦线、正切线 | |
| B. | 总能分别作出正弦线、余弦线、正切线,但可能不只一条 | |
| C. | 正弦线、余弦线、正切线都可能不存在 | |
| D. | 正弦线、余弦线总存在,但正切线不一定存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤-4 | B. | -4≤a≤6 | C. | a≤-4或a≥6 | D. | a≥6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
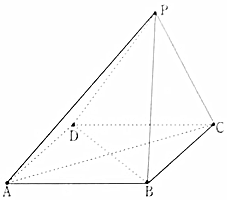 已知在四棱锥P-ABCD中,底面ABCD是平行四边形,且有PB=PD,PA⊥BD.
已知在四棱锥P-ABCD中,底面ABCD是平行四边形,且有PB=PD,PA⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 古文迷 | 非古文迷 | 合计 | |
| 男生 | 26 | 24 | 50 |
| 女生 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com