练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
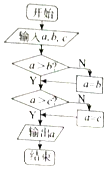
    20．执行如图所示的程序框图，若输入三个数a=log36，b=log48，c=1.22，则输出的结果为（　　）
    A．log36B．log48C．1.22D．log23

    分析 模拟程序的运行，可得程序框图的功能是输出三个数中最大的数，利用指数函数与对数函数的单调性与1.5相比较即可得出．

    解答 解：模拟程序的运行，可得程序框图的功能是输出三个数中最大的数，
    ∵a=log36=1+log32＞1+log3$\sqrt{3}$=1.5，
    b=log48=$\frac{lg8}{lg4}$=$\frac{3lg2}{2lg2}$=$\frac{3}{2}$=1.5．
    c=1.22=1.44，
    ∴可得：c＜b＜a．
    故选：A．

    点评 本题考查了程序框图的应用，指数函数与对数函数的单调性，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．下列命题中真命题的个数是（　　）
    ①函数y=sinx，其导函数是偶函数；
    ②“若x=y，则x2=y2”的逆否命题为真命题；
    ③“x≥2”是“x2-x-2≥0”成立的充要条件；
    ④命题p：“?x0∈R，x02-x0+1＜0”，则命题p的否定为：“?x∈R，x2-x+1≥0”．
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

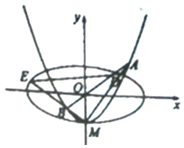    11．如图，已知椭圆C1：$\frac{x^2}{4}+{y^2}=1$，曲线C2：y=x2-1与y轴的交点为M，过坐标原点O的直线l与C2相交于A，B两点，直线MA，MB分别与C1相交于D，E两点，则$\overrightarrow{ME}•\overrightarrow{MD}$的值是（　　）
    A．正数B．0C．负数D．皆有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某市房产契税标准如下：
    购房总价（万）（0，200]（200，400]（400，+∞）
    税率1%1.5%3%
    从该市某高档住宅小区，随机调查了一百户居民，获得了他们的购房总额数据，整理得到了如下的频率分布直方图：

    （Ⅰ）假设该小区已经出售了2000套住房，估计该小区有多少套房子的总价在300万以上，说明理由．
    （Ⅱ）假设同组中的每个数据用该组区间的右端点值代替，估计该小区购房者缴纳契税的平均值．

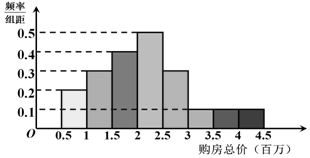
    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

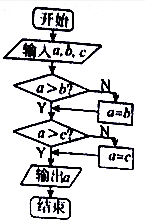
    15．执行如图所示的程序框图，若输入三个数a=log36，b=log510，c=log714，则输出的结果为（　　）
    A．log36B．log510C．log714D．log26

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．若集合A={x|x（x-1）＜2}，且A∪B=A，则集合B可能是（　　）
    A．{-1，2}B．{0，1}C．{-1，0}D．{0，2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数$f（x）=tan（x+\frac{π}{4}）$．
    （Ⅰ）求f（x）的定义域；
    （Ⅱ）设β∈（0，π），且$f（β）=2cos（β-\frac{π}{4}）$，求β的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．设{an}是首项为1，公差为2的等差数列，{bn}是首项为1，公比为q的等比数列．记cn=an+bn，n=1，2，3，…．
    （1）若{cn}是等差数列，求q的值；
    （2）求数列{cn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．学校为了了解高三学生每天自主学习中国古典文学的时间，随机抽取了高三男生和女生各50名进行问卷调查，其中每天自主学习中国古典文学的时间超过3小时的学生称为“古文迷”，否则为“非古文迷”，调查结果如表：
    古文迷非古文迷合计
    男生262450
    女生302050
    合计5644100
    （Ⅰ）根据表中数据能否判断有60%的把握认为“古文迷”与性别有关？
    （Ⅱ）现从调查的女生中按分层抽样的方法抽出5人进行调查，求所抽取的5人中“古文迷”和“非古文迷”的人数；
    （Ⅲ）现从（Ⅱ）中所抽取的5人中再随机抽取3人进行调查，记这3人中“古文迷”的人数为ξ，求随机变量ξ的分布列与数学期望．
    参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
    参考数据：
    P（K2≥k0）0.500.400.250.050.0250.010
    k00.4550.7081.3213.8415.0246.635

    查看答案和解析>>

    同步练习册答案