
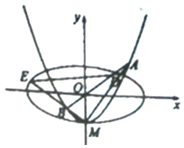
 如图,已知椭圆C1:$\frac{x^2}{4}+{y^2}=1$,曲线C2:y=x2-1与y轴的交点为M,过坐标原点O的直线l与C2相交于A,B两点,直线MA,MB分别与C1相交于D,E两点,则$\overrightarrow{ME}•\overrightarrow{MD}$的值是( )
如图,已知椭圆C1:$\frac{x^2}{4}+{y^2}=1$,曲线C2:y=x2-1与y轴的交点为M,过坐标原点O的直线l与C2相交于A,B两点,直线MA,MB分别与C1相交于D,E两点,则$\overrightarrow{ME}•\overrightarrow{MD}$的值是( )| A. | 正数 | B. | 0 | C. | 负数 | D. | 皆有可能 |
分析 由题意设出A,B的坐标,再设出过原点的直线l的方程,联立直线方程与抛物线方程,利用根与系数的关系可得$\overrightarrow{MA}•\overrightarrow{MB}=0$,再结合$\overrightarrow{MD}=λ\overrightarrow{MA}$,$\overrightarrow{ME}=μ\overrightarrow{MB}$得答案.
解答 解:设A(x1,y1),B(x2,y2),
过原点的直线l:y=tx,
联立$\left\{\begin{array}{l}{y=tx}\\{y={x}^{2}-1}\end{array}\right.$,得x2-tx-1=0.
则x1+x2=t,x1x2=-1.
∴$\overrightarrow{MA}•\overrightarrow{MB}=({x}_{1},{y}_{1}+1)•({x}_{2},{y}_{2}+1)$=x1x2+(y1+1)(y2+1)
=(t2+1)x1x2+t(x1+x2)+1=-(t2+1)+t2+1=0.
而$\overrightarrow{MD}=λ\overrightarrow{MA}$,$\overrightarrow{ME}=μ\overrightarrow{MB}$,
∴$\overrightarrow{ME}•\overrightarrow{MD}$=$λμ\overrightarrow{MA}•\overrightarrow{MB}=0$.
故选:B.
点评 本题考查椭圆与抛物线的简单性质,考查向量在求解圆锥曲线问题中的应用,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (2,-2) | B. | (2,2) | C. | (-2,-2) | D. | (-2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{2}$ | B. | $\sqrt{31}$ | C. | $\sqrt{33}$ | D. | $4\sqrt{2}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
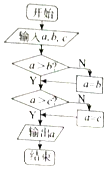 执行如图所示的程序框图,若输入三个数a=log36,b=log48,c=1.22,则输出的结果为( )
执行如图所示的程序框图,若输入三个数a=log36,b=log48,c=1.22,则输出的结果为( )| A. | log36 | B. | log48 | C. | 1.22 | D. | log23 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|x≥-1} | C. | {x|0<x≤1} | D. | {x|-1≤x≤1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com