
分析 (Ⅰ)构造函数g(x)=f(x)-(1-λ)x-λ,根据导数和函数的最值即可证明,
(Ⅱ)对任意实数λ,总存在实数x∈[-3,3],有f(x)>λ等价于f(x)的最大值大于λ,求导后,分类讨,根据导数和函数的最值得关系即可证明
解答 解:(Ⅰ)设g(x)=f(x)-(1-λ)x-λ=x+$\frac{λ}{e^x}$-(1-λ)x-λ=λ($\frac{1}{{e}^{x}}$-x-1),
∴g′(x)=λ(1-$\frac{1}{{e}^{x}}$),
令g′(x)=0,解得x=0,
当x>0时,g′(x)>0,函数g(x)单调递增,
当x<0时,g′(x)<0,函数g(x)单调递减,
∴g(x)min=g(0)=0,
∴f(x)≥(1-λ)x+λ,当x=0时取等号,
(Ⅱ)证明:“对任意实数λ,总存在实数x∈[-3,3],有f(x)>λ等价于f(x)的最大值大于λ.
∵f′(x)=1-λe-x,
∴当λ≤0时,x∈[-3,3],f′(x)>0,f(x)在[-3,3]上单调递增,
∴f(x)的最大值为f(3)>f(0)=λ.
∴当λ≤0时命题成立;
当λ>0时,由f′(x)=0得x=lnλ,
则x∈R时,x,f′(x),f(x)关系如下:
| x | (-∞,0) | lna | (0,+∞) |
| f(x) | - | 0 | + |
| f′(x) | ↓ | 极小值 | ↑ |
点评 本题考查了导数和函数的最值,以及不等式的证明,考查了分类讨论的思想,考查了学生的运算能力和转化能力,属于难题


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:解答题
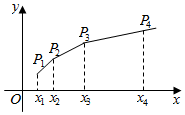 已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.
已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
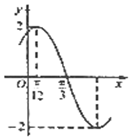 已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,下列说法正确的有( )个
已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,下列说法正确的有( )个| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com