考点:函数零点的判定定理,利用导数研究函数的单调性
专题:函数的性质及应用
分析:整理函数f(x),令g(x)=a1(x-λ2)(x-λ3)+a2(x-λ1)(x-λ3)+a3(x-λ1)(x-λ2),由函数零点存在判定定理可知:在区间(λ1,λ2),(λ2,λ3)内分别存在一个零点;又函数g(x)是二次函数,最多有两个零点,即可判断出.
解答:
解:f(x)=
++=
| a1(x-λ2)(x-λ3)+a2(x-λ1)(x-λ3)+a3(x-λ1)(x-λ2) |
| (x-λ1)(x-λ2)(x-λ3) |
令g(x)=a
1(x-λ
2)(x-λ
3)+a
2(x-λ
1)(x-λ
3)+a
3(x-λ
1)(x-λ
2),
∵λ
1<λ
2<λ
3,
∴g(λ
1)=a
1(λ
1-λ
2)(λ
1-λ
3)>0,
g(λ
2)=a
2(λ
2-λ
1)(λ
2-λ
3)<0,
g(λ
3)=a
3(λ
3-λ
1)(λ
3-λ
2)>0,
由函数零点存在判定定理可知:在区间(λ
1,λ
2),(λ
2,λ
3)内分别存在一个零点;
又函数g(x)是二次函数,最多有两个零点,
因此函数g(x)的两个零点分别位于区间(λ
1,λ
2),(λ
2,λ
3)内.
故函数f(x)=
++的两个零点分别位于区间(λ
1,λ
2),(λ
2,λ
3)内.
故选:B.
点评:本题主要考查函数的零点的判定定理的应用,根据函数的解析式求函数的值,判断函数的零点所在的区间的方法,属于基础题.



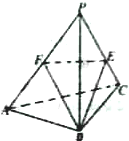 如图:已知正三棱锥P-ABC,侧棱PA,PB,PC的长为2,且∠APB=30°,E,F分别是侧棱PC,PA上的动点,则△BEF的周长的最小值为( )
如图:已知正三棱锥P-ABC,侧棱PA,PB,PC的长为2,且∠APB=30°,E,F分别是侧棱PC,PA上的动点,则△BEF的周长的最小值为( ) 如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.
如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.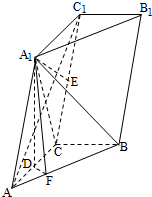 如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.