
分析 通过数列找出规律:该数列中(-1)nn会出现n个,n∈N*,即该数列前100中会出现13个-13,9个14,计算即可.
解答 解:由题意可知该数列中(-1)nn会出现n个,n∈N*,
∵$\frac{13×(13+1)}{2}$=91<100,$\frac{14×(14+1)}{2}$=105>100,
∴该数列前100中会出现13个-13,9个14,
∴S100=-1+2×2-3×3+4×4-5×5+6×6-7×7+8×8-9×9+10×10-11×11+12×12-13×13+9×14
=-1+(2-3)(2+3)+(4-5)(4+5)+(6-7)(6+7)+(8-9)(8+9)+(10-11)(10+11)+(12-13)(12+13)+9×14
=-1-5-9-13-17-21-25+126
=126-91
=35,
故答案为:35.
点评 本题考查其数列的通项,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
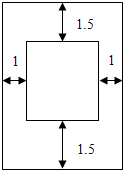 某出版社出版一读物,为了排版设计的需要,规定:一页上所印文字的矩形区域需要占去150cm2,上、下边各要留1.5cm宽的空白,左、右两边各要留1cm宽的空白,出版商为了节约纸张,应选用怎样尺寸的矩形纸张来设计版面?
某出版社出版一读物,为了排版设计的需要,规定:一页上所印文字的矩形区域需要占去150cm2,上、下边各要留1.5cm宽的空白,左、右两边各要留1cm宽的空白,出版商为了节约纸张,应选用怎样尺寸的矩形纸张来设计版面?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\{x|x<-\frac{1}{3}或x>\frac{1}{2}\}$ | B. | $\{x|-\frac{1}{3}<x<\frac{1}{2}\}$ | C. | $\{x|x>\frac{1}{2}\}$ | D. | $\{x|x>-\frac{1}{3}\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com