
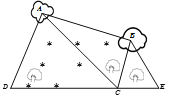
【题目】如图,为了测量某湿地![]() 两点间的距离,观察者找到在同一直线上的三点
两点间的距离,观察者找到在同一直线上的三点![]() .从
.从![]() 点测得
点测得![]() ,从
,从![]() 点测得
点测得![]() ,
,![]() ,从
,从![]() 点测得
点测得![]() .若测得
.若测得![]() ,
,![]() (单位:百米),则
(单位:百米),则![]() 两点的距离为( )
两点的距离为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据题意,在△ADC中,分析角边关系可得AC=DC=2![]() ,在△BCE中,由正弦定理可得BC的值,据此在△ABC中,利用余弦定理分析可得答案.
,在△BCE中,由正弦定理可得BC的值,据此在△ABC中,利用余弦定理分析可得答案.
根据题意,在△ADC中,∠ACD=45°,∠ADC=67.5°,DC=2![]() ,
,
则∠DAC=180°﹣45°﹣67.5°=67.5°,则AC=DC=2![]() ,
,
在△BCE中,∠BCE=75°,∠BEC=60°,CE![]() ,
,
则∠EBC=180°﹣75°﹣60°=45°,
则有![]() ,变形可得BC
,变形可得BC ,
,
在△ABC中,AC=2![]() ,BC
,BC![]() ,∠ACB=180°﹣∠ACD﹣∠BCE=60°,
,∠ACB=180°﹣∠ACD﹣∠BCE=60°,
则AB2=AC2+BC2﹣2ACBCcos∠ACB=9,
则AB=3;
故选:C.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() ,
,![]() 为曲线
为曲线![]() 上的一动点.
上的一动点.
(I)求动点![]() 对应的参数从
对应的参数从![]() 变动到
变动到![]() 时,线段
时,线段![]() 所扫过的图形面积;
所扫过的图形面积;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 为线段
为线段![]() 的中点?若存在,求出点
的中点?若存在,求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的方程为
的方程为![]() .
.
(1)以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设曲线
,设曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,曲线
,曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线![]() 与曲线
与曲线![]() 满足下列两个条件:①直线
满足下列两个条件:①直线![]() 在点
在点![]() 处与曲线
处与曲线![]() 相切;②曲线
相切;②曲线![]() 在点
在点![]() 附近位于直线
附近位于直线![]() 的两侧,则称直线
的两侧,则称直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]() .则下列结论正确的是( )
.则下列结论正确的是( )
A.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
B.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
C.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
D.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com