
| A. | [0,$\frac{π}{3}}$] | B. | [$\frac{5π}{6}$,π] | C. | [$\frac{π}{3}$,$\frac{5π}{6}}$] | D. | 以上都不是 |
分析 根据函数奇偶性及诱导公式得出$α=-\frac{π}{2}$,利用正弦函数的单调性列方程组解出y=-sin(2x+$\frac{1}{3}$α)的增区间即可.
解答 解:∵y=cos(2x+α)(x∈R)是奇函数,
∴α=$\frac{π}{2}$+kπ,k∈Z.∵-π<α<0,∴α=$-\frac{π}{2}$.
∴y=-sin(2x+$\frac{1}{3}$α)=-sin(2x-$\frac{π}{6}$).
令$\frac{π}{2}+2kπ$≤2x-$\frac{π}{6}$$≤\frac{3π}{2}+2kπ$,解得$\frac{π}{3}$+kπ≤x≤$\frac{5π}{6}$+kπ,k∈Z.
∵x∈[0,π],∴$\frac{π}{3}≤x≤\frac{5π}{6}$.
∴y=-sin(2x+$\frac{1}{3}$α)在[0,π]上的增区间是[$\frac{π}{3}$,$\frac{5π}{6}$].
故选:C.
点评 本题考查了正弦函数的性质,诱导公式的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [$\frac{1}{5}$,1] | C. | (1,+∞)∪(-∞,$\frac{1}{5}$) | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
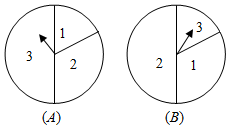 如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ.
如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
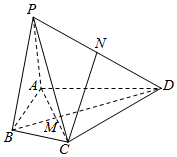 如图,在四棱锥P-ABCD中,△ACD是正三角形,BD垂直平分AC,垂足为M,∠ABC=120°,PA=AB=1,PD=2,N为PD的中点.
如图,在四棱锥P-ABCD中,△ACD是正三角形,BD垂直平分AC,垂足为M,∠ABC=120°,PA=AB=1,PD=2,N为PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com