
| A. | 2 | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | 6 |
分析 由已知得$<\overrightarrow{a},\overrightarrow{b}>=<\overrightarrow{a},\overrightarrow{c}>=<\overrightarrow{b},\overrightarrow{c}>=12{0}^{0}$,即$\overrightarrow{a}•\overrightarrow{c}=\overrightarrow{b}•\overrightarrow{c}$,$(\overrightarrow a-\overrightarrow b)•\overrightarrow m$=$(\overrightarrow{a}-\overrightarrow{b})•(\overrightarrow{a}-2017\overrightarrow{c})$=${\overrightarrow{a}}^{2}-2017\overrightarrow{a}•\overrightarrow{c}-\overrightarrow{a}•\overrightarrow{b}+2017\overrightarrow{b}•\overrightarrow{c}$=4-$\overrightarrow{a}•\overrightarrow{b}$=4-2×2×cos120°=6
解答 解:∵平面向量$\vec a,\vec b,\vec c$不共线,且两两所成的角相等,|$\overrightarrow a|=|\overrightarrow b|=2,|\overrightarrow c|=1$,
∴$<\overrightarrow{a},\overrightarrow{b}>=<\overrightarrow{a},\overrightarrow{c}>=<\overrightarrow{b},\overrightarrow{c}>=12{0}^{0}$,即$\overrightarrow{a}•\overrightarrow{c}=\overrightarrow{b}•\overrightarrow{c}$,
$(\overrightarrow a-\overrightarrow b)•\overrightarrow m$=$(\overrightarrow{a}-\overrightarrow{b})•(\overrightarrow{a}-2017\overrightarrow{c})$=${\overrightarrow{a}}^{2}-2017\overrightarrow{a}•\overrightarrow{c}-\overrightarrow{a}•\overrightarrow{b}+2017\overrightarrow{b}•\overrightarrow{c}$=4-$\overrightarrow{a}•\overrightarrow{b}$=4-2×2×cos120°=6
故选:D
点评 本题考查了平面向量的数量积运算,属于基础题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
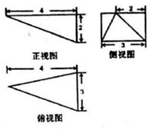 某几何体的三视图如图所示,则该几何体中最长的棱长为( )
某几何体的三视图如图所示,则该几何体中最长的棱长为( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{21}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{b}{a}$ | D. | $\frac{a}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{9}{2}$π+24 | B. | $\frac{9}{2}$π+30 | C. | 9π+54 | D. | 36π+30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-$\frac{3}{2}$)2+y2=25 | B. | (x+$\frac{3}{2}$)2+y2=$\frac{1}{4}$ | C. | (x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$ | D. | x2+(y-$\frac{3}{2}$)2=$\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com