
| A. | 等差数列 | B. | 等比数列 | ||
| C. | 既不是等差数列,也不是等比数列 | D. | 既是等差数列,又是等比数列 |
分析 根据题意,由数列an}的前n项和公式计算可得数列{an}的通项公式,结合等差数列、等比数列的定义分析可得答案.
解答 解:根据题意,数列{an}的前n项和为Sn=aqn,
当n=1时,a1=S1=aq;
当n≥2时,an=Sn-Sn-1=aqn-1(q-1),
数列{an}不是等差数列,
又由$\frac{{a}_{n+1}}{{a}_{n}}$=q(q≠1,q为非零常数),而$\frac{{a}_{2}}{{a}_{1}}$=q-1≠q,
数列{an}不是等比数列,
故数列{an}既不是等差数列,也不是等比数列,
故选C.
点评 本题考查等比数列、等差数列的判定,关键是求出数列{an}的通项公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 15 | 30 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 模型1对应的R2=0.48 | B. | 模型3对应的R2=0.15 | ||
| C. | 模型2对应的R2=0.96 | D. | 模型4对应的R2=0.30 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
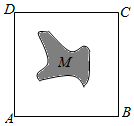 如图,面积为S的正方形ABCD中有一个不规则的图形M,可以用随机模拟方法近似计算M的面积,在正方向ABCD中随机投掷3600个点,若恰好有1200个点落入M中,则M的面积的近似值为$\frac{S}{3}$.
如图,面积为S的正方形ABCD中有一个不规则的图形M,可以用随机模拟方法近似计算M的面积,在正方向ABCD中随机投掷3600个点,若恰好有1200个点落入M中,则M的面积的近似值为$\frac{S}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com