已知数列
前
项和
，
（1）求其通项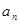
；（2）若它的第
项满足
，求的值。
科目：高中数学 来源： 题型：解答题
某企业为加大对新产品的推销力度，决定从今年起每年投入100万元进行广告宣传，以增加新产品的销售收入．已知今年的销售收入为250万元，经市场调查，预测第n年与第n－1年销售收入an与an－1(单位：万元)满足关系式：an＝an－1＋
－100.
(1)设今年为第1年，求第n年的销售收入an；
(2)依上述预测，该企业前几年的销售收入总和Sn最大．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（2） 
求
,求出
和
,而后验证是否可以合为一个通项公式．
的不等式,可得
．
时则有
；
时,
; 
,有
成立;
,
．
中，
，
，
，则该数列的通项为 。
中，
，其中
。
的值；
的前
项和为
满足
，且
.
的值；
中各项均为正，有
,
，
中，
，点
在直线
上．
和
的值；（2）求数列
和
；
，求数列
的前n项和
．
，
满足
，
，
，数列
项和为
，
.
；
时，
．
，
，且
，
．
，证明数列{bn}是等比数列；
，求集合
．
中满足
，
.
和公差
；