
已知等比数列 中各项均为正,有
中各项均为正,有 ,
, ,
,
等差数列 中,
中, ,点
,点 在直线
在直线 上.
上.
(1)求 和
和 的值;(2)求数列
的值;(2)求数列 ,
, 的通项
的通项 和
和 ;
;
(3)设 ,求数列
,求数列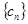 的前n项和
的前n项和 .
.
科目:高中数学 来源: 题型:填空题
① 是数列
是数列 的前
的前 项和,若
项和,若 ,则数列
,则数列 是等差数列
是等差数列
②若 ,则
,则
③已知函数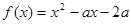 ,若存在
,若存在 ,使得
,使得 成立,则
成立,则
④在 中,
中, 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 则
则 为等腰直角三角形
为等腰直角三角形
其中正确的有 (填上所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高一学生1000人,每周一次同时在两个可容纳600人的会议室,开设“音乐欣赏”与“美术鉴赏”的校本课程.要求每个学生都参加,要求第一次听“音乐欣赏”课的人数为
 ,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用
,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用 分别表示在第
分别表示在第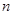 次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
(1)若 ,分别求出第二次,第三次选“音乐欣赏”课的人数
,分别求出第二次,第三次选“音乐欣赏”课的人数 ;
;
(2)①证明数列 是等比数列,并用
是等比数列,并用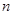 表示
表示 ;
;
②若要求前十次参加“音乐欣赏”课的学生的总人次不超过5800,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知{an}是一个公差大于0的等差数列,且满足a4a5=55,a3+a6=16
(1)求数列{an}的通项公式;
(2)若数列{an}和数列{bn}满足等式:
an-1= ,an=
,an= (
(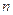 为正整数),
为正整数),
设数列{bn}的前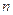 项和
项和 ,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn,
,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn,
求Tn的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
称满足以下两个条件的有穷数列 为
为 阶“期待数列”:
阶“期待数列”:
① ;②
;② .
.
(1)若等比数列 为
为 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 的通项公式;
的通项公式;
(2)若一个等差数列 既是
既是 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记n阶“期待数列”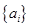 的前k项和为
的前k项和为 :
:
(i)求证: ;
;
(ii)若存在 使
使 ,试问数列
,试问数列 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com