Question

20．若关于x的不等式a≤$\frac{3}{4}$x²-3x+4≤b的解集恰好为[a，b]，那么b-a=4．

Answer 1

分析 画出函数f（x）=$\frac{3}{4}$x²-3x+4的图象，可知f（x）_min=1；分类讨论：a＞1时，不等式a≤$\frac{3}{4}$x²-3x+4≤b的解集分为两段区域，不符合题意；
有a≤1＜b，再利用f（a）=f（b）=b，解得a，b的值．

解答 解：画出函数f（x）=$\frac{3}{4}$x²-3x+4=$\frac{3}{4}$（x-2）²+1的图象，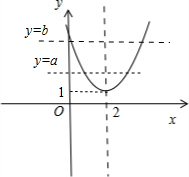
可得f（x）_min=f（2）=1，
由图象可知：若a＞1，则不等式a≤$\frac{3}{4}$x²-3x+4≤b的解集分两段区域，不符合已知条件，
因此a≤1，此时a≤x²-3x+4恒成立；
又∵不等式a≤$\frac{3}{4}$x²-3x+4≤b的解集为[a，b]，
∴a≤1＜b，f（a）=f（b）=b，可得$\left\{\begin{array}{l}{{\frac{3}{4}a}^{2}-3a+4=b}\\{{\frac{3}{4}b}^{2}-3b+4=b}\end{array}\right.$，
由$\frac{3}{4}$b²-3b+4=b，化为3b²-16b+16=0，解得b=$\frac{4}{3}$或b=4；
当b=$\frac{4}{3}$时，由$\frac{3}{4}$a²-3a+4-$\frac{4}{3}$=0，解得a=$\frac{4}{3}$或a=$\frac{8}{3}$，不符合题意，舍去；
∴b=4，此时a=0；
∴b-a=4．
故答案为：4．

点评 本题考查了二次函数的图象与性质、一元二次不等式的解法与应用问题，也考查了分类讨论思想与推理计算能力，是较难的题目．