
分析 (1)利用查三角恒等变换化简函数的解析式,再利用余弦函数的周期性,求得函数f(x)的最小正周期.
(2)利用余弦函数的定义域和值域,求得函数f(x)在区间[$\frac{π}{16}$,$\frac{3π}{16}$]上的最小值及取最小值时对应的x的值.
解答 解:(1)∵f(x)=2sin4x+2cos4x+cos22x-$\sqrt{3}$sin4x=2(sin2x+cos2x)2-4sin2x•cos2x+cos22x-$\sqrt{3}$sin4x
=2-sin22x+cos22x-$\sqrt{3}$sin4x=2+cos4x-$\sqrt{3}$sin4x=2+2cos(4x+$\frac{π}{3}$),
故函数f(x)的最小正周期为$\frac{2π}{4}$=$\frac{π}{2}$.
(2)在区间[$\frac{π}{16}$,$\frac{3π}{16}$]上,4x+$\frac{π}{3}$∈[$\frac{7π}{12}$,$\frac{13π}{12}$],故当4x+$\frac{π}{3}$=π时,函数f(x)取得最小值为2-2=0,
此时,x=$\frac{π}{6}$.
点评 本题主要考查三角恒等变换,余弦函数的值域、定义域和值域,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
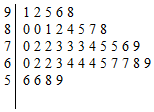 中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )
中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 3 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 12 | C. | 26 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{10})$ | B. | $(\sqrt{10},+∞)$ | C. | $({1,\sqrt{10}}]$ | D. | $[{\sqrt{10}}\right.,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com