
| A. | -6 | B. | 3 | C. | 6 | D. | 8 |
分析 根据条件即可求出$|\overrightarrow{a}||\overrightarrow{b}|=2\sqrt{5}•\sqrt{9+{m}^{2}}$,$\overrightarrow{a}•\overrightarrow{b}=-6-4m$,代入$|\overrightarrow{a}||\overrightarrow{b}|+\overrightarrow{a}•\overrightarrow{b}=0$即可得出关于m的方程,解出m即可.
解答 解:$|\overrightarrow{a}||\overrightarrow{b}|=2\sqrt{5}•\sqrt{9+{m}^{2}}$,$\overrightarrow{a}•\overrightarrow{b}=-6-4m$;
又$|\overrightarrow{a}||\overrightarrow{b}|+\overrightarrow{a}•\overrightarrow{b}=0$;
∴$2\sqrt{5}•\sqrt{9+{m}^{2}}-6-4m=0$;
∴$\sqrt{5}•\sqrt{9+{m}^{2}}=3+2m$,两边平方并整理得:
m2-12m+36=0;
解得m=6.
故选:C.
点评 考查根据向量坐标求向量长度的方法,向量数量积的坐标运算,无理方程的求法.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于y轴对称 | B. | 关于原点对称 | ||
| C. | 关于直线x+y=0对称 | D. | 关于直线x-y=0对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
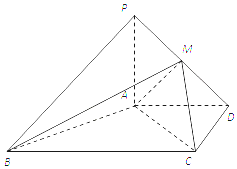 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com