
分析 画出约束条件的可行域,化简目标函数,转化为直线的斜率问题,通过函数的值域求解目标函数的范围即可.
解答  解:约束条件的可行域如图:由$\left\{\begin{array}{l}{x+y=0}\\{x+3y=3}\end{array}\right.$可得A(-$\frac{3}{2}$,$\frac{3}{2}$),
解:约束条件的可行域如图:由$\left\{\begin{array}{l}{x+y=0}\\{x+3y=3}\end{array}\right.$可得A(-$\frac{3}{2}$,$\frac{3}{2}$),
$\left\{\begin{array}{l}{x-y=0}\\{x+3y=3}\end{array}\right.$可得B($\frac{3}{4}$,$\frac{3}{4}$),
则$\frac{x+y}{\sqrt{{x}^{2}+{y}^{2}}}$=$\sqrt{1+\frac{2xy}{{x}^{2}+{y}^{2}}}$=$\sqrt{1+\frac{2}{\frac{y}{x}+\frac{x}{y}}}$,由题意可得$\frac{y}{x}$∈[-1,1],令t=$\frac{y}{x}$∈[-1,1],则$\frac{y}{x}+\frac{x}{y}$=t+$\frac{1}{t}$∈[2,+∞)∪(-∞,-2],
∴$\sqrt{1+\frac{2}{\frac{y}{x}+\frac{x}{y}}}$∈[0,2].
故答案为:[0,2].
点评 本题考查线性规划的简单应用,考查数形结合以及函数的最值的求法,考查转化思想以及计算能力.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
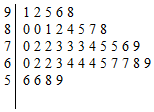 中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )
中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 3 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{4}{5}$ | C. | -i | D. | $\frac{4}{5}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com