
分析 设A(x1,y1),B(x2,y2),由抛物线的定义,得|AF|=x1+1,|BF|=x2+1.又根据中点坐标公式,可得x1+x2=8,代入前式即可得到|AF|+|BF|的值.
解答 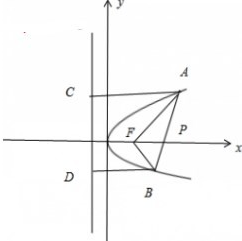 解:设A(x1,y1),B(x2,y2),
解:设A(x1,y1),B(x2,y2),
作出抛物线的准线:x=-1,过A、B分别作准线的垂线,垂足分别为C、D,
根据抛物线的定义,得
|AF|=|AC|=x1+1,|BF|=|BD|=x2+1,故|AF|+|BF|=(x1+x2)+2
∵AB中点为P(4,1),
∴$\frac{1}{2}$(x1+x2)=4,可得x1+x2=8
∴|AF|+|BF|=(x1+x2)+2=10
故答案为:10.
点评 本题给出抛物线的弦AB的中点坐标,求A、B两点到焦点距离之和,着重考查了抛物线的定义、标准方程和简单几何性质等知识,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
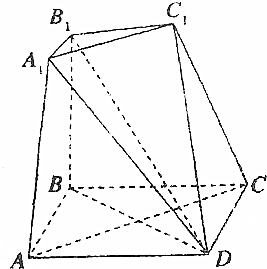 如图所示的七面体是由三棱台ABC-A1B1C1和四棱锥D-AA1C1C对接而成,四边形ABCD是边长为2的正方形,BB1⊥平面⊥ABCD,BB1=2A1B1=2.
如图所示的七面体是由三棱台ABC-A1B1C1和四棱锥D-AA1C1C对接而成,四边形ABCD是边长为2的正方形,BB1⊥平面⊥ABCD,BB1=2A1B1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年龄x | 6 | 7 | 8 | 9 |
| 身高y | 118 | 126 | 136 | 144 |
| A. | 65 | B. | 74 | C. | 56 | D. | 47 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0<0,e${\;}^{{x}_{0}}$+2x0-1<0 | B. | ?x≥0,ex+2x-1<0 | ||
| C. | ?x0≥0,e${\;}^{{x}_{0}}$+2x0-1<0 | D. | ?x0<0,e${\;}^{{x}_{0}}$+2x0-1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com