练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．若sinxcosy+cosxsiny=$\frac{1}{2}$，cos2x-cos2y=$\frac{2}{3}$，则sin（x-y）=-$\frac{2}{3}$．

    分析 利用两角差的正弦公式求得sin（x+y）=$\frac{1}{2}$，再利用和差化积公式可得-2sin（x+y）sin（x-y）=$\frac{2}{3}$，由此求得sin（x-y）的值．

    解答 解：∵sinxcosy+cosxsiny=sin（x+y）=$\frac{1}{2}$，cos2x-cos2y=-2sin（x+y）sin（x-y）=$\frac{2}{3}$，
    ∴-2•$\frac{1}{2}$•sin（x-y）=$\frac{2}{3}$，∴sin（x-y）=-$\frac{2}{3}$，
    故答案为：-$\frac{2}{3}$．

    点评 本题主要考查两角差的正弦公式，和差化积公式的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．一个四棱锥的三视图如图所示，则此四棱锥的体积为（　　）
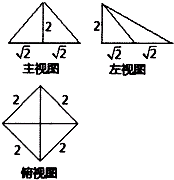
    A．$\frac{8}{3}$B．$\frac{4}{3}$C．$\frac{{4\sqrt{2}}}{3}$D．$\frac{5}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=|x-a|+|x-2a|．
    （Ⅰ）对任意x∈R，不等式f（x）＞1成立，求实数a的取值范围；
    （Ⅱ）当a=-1时，解不等式f（x）＜3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．数列{an}为等比数列，前n项和记为Sn，若Sn=kn+rm（k，r∈R，m∈Z），则下列叙述正确的是（　　）
    A．r=1，m为偶数B．r=1，m为奇数C．r=-1，m为偶数D．r=-1，m为奇数

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知椭圆方程：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），F1（-1，0），F2（1，0）分别是椭圆的左右焦点，P为椭圆上的点，△PF1F2的内切圆为⊙O1，△PF1F2的外接圆为⊙O2，若∠F1PF2=30°时，⊙O1的半径为2-$\sqrt{3}$．
    （1）求椭圆方程；
    （2）设⊙O2的面积为S2，⊙O1的面积为S1，求$\frac{{S}_{2}}{{S}_{1}}$的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．设抛物线y2=4x焦点F，经过点P（4，1）的直线l与抛物线相交于A、B两点，且点P恰好为线段AB的中点，则|AF|+|BF|=10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．双曲线$\frac{{x}^{2}}{m}$-y2=1的右焦点与抛物线y2=8x的焦点重合，该双曲线的渐近线为y=±$\frac{\sqrt{3}}{3}$x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．若运行如图所示程序框图，则输出结果S的值为（　　）
    A．$\frac{3}{7}$B．$\frac{4}{9}$C．$\frac{9}{20}$D．$\frac{5}{11}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．向量的运算常常与实数运算进行类比，下列类比推理中结论正确的是（　　）
    A．“若ac=bc（c≠0），则a=b”类比推出“若$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$（$\overrightarrow{c}$≠$\overrightarrow{0}$），则$\overrightarrow{a}$=$\overrightarrow{b}$”
    B．“在实数中有（a+b）c=ac+bc”类比推出“在向量中（$\overrightarrow{a}$+$\overrightarrow{b}$）•$\overrightarrow{c}$=$\overrightarrow{a}$•$\overrightarrow{c}$+$\overrightarrow{b}$•$\overrightarrow{c}$”
    C．“在实数中有（ab）c=a（bc）”类比推出“在向量中（$\overrightarrow{a}$•$\overrightarrow{b}$）•$\overrightarrow{c}$=$\overrightarrow{a}$•（$\overrightarrow{b}$•$\overrightarrow{c}$）”
    D．“若ab=0，则a=0或b=0”类比推出“若$\overrightarrow{a}$•$\overrightarrow{b}$=0，则$\overrightarrow{a}$=$\overrightarrow{0}$或$\overrightarrow{b}$=$\overrightarrow{0}$”

    查看答案和解析>>

    同步练习册答案