考点:直线与平面所成的角
专题:空间角
分析:(1)由已知条件推导出△A1BC为正三角形,A1B=BC=2,由此能求出棱柱的高.
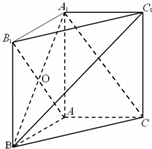
(2)连结AB1,A1B∩AB1=O,由已知条件推导出∠B1C1O是B1C1与平面A1BC1所成的角平面角,由此能求出B1C1与平面A1BC1所成的角的大小.
解答:
解:(1)∵在直三棱柱ABC-A
1B
1C
1中,AC=AB=
,∠BAC=90°,
∴Rt△A
1AB≌Rt△A
1AC,∴A
1B=A
1C,…2 分
又∵异面直线A
1B与B
1C
1所成的角等于60°,
∴A
1BC=60°,∴△A
1BC为正三角形,
∵AC=AB=
,∠BAC=90°,
∴A
1B=BC=
=2,…4 分
∴BB
1=
=
,即棱柱的高BB
1=
.
(2)连结AB
1,A
1B∩AB
1=O,
∵B
1O⊥A
1B,B
1O⊥AC,
∴B
1O⊥面A
1BC
1,∴∠B
1C
1O是B
1C
1与平面A
1BC
1所成的角平面角,
在Rt△B
1C
1O中,B
1O=1,B
1C
1=2,
∴sin∠B
1C
1O=
=
,
∴
∠B1C1O=,
∴B
1C
1与平面A
1BC
1所成的角为
.
点评:本题考查棱柱的高的求法,考查直线与平面所成的角的求法,解题时要认真审题,注意空间思维能力的培养.

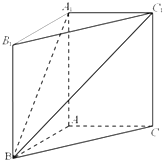 如图,在直三棱柱ABC-A1B1C1中,AC=AB=
如图,在直三棱柱ABC-A1B1C1中,AC=AB= 解:(1)∵在直三棱柱ABC-A1B1C1中,AC=AB=
解:(1)∵在直三棱柱ABC-A1B1C1中,AC=AB=

 名校课堂系列答案
名校课堂系列答案