解答:
解:(Ⅰ)令f'(x)=2
n-1nx
n-1-n(a+x)
n-1=0
得(2x)
n-1=(a+x)
n-1,∴2x=a+x,∴x=a---------------(2分)
当0≤x≤a时,∴2x<a+x,∴f'(x)≤0,故f(x)在[0,a]上递减.
当x>a,f'(x)>0,故f(x)在(a,+∞)上递增.
∴,当x=a时,f(x)的最小值为f(a)=0---------------(4分)
(Ⅱ)由b>0,有f(x)≥f(a)=0,即f(b)=2
n-1(a
n+b
n)-(a+b)
n≥0
故
≥()n(a>0,b>0,n∈N*).--------(5分)
(Ⅲ)证明:要证:
≥()n只要证:
(k+1)n-1(+++…+)≥(a1+a2+a3+…+ak+1)n设
g(x)=(k+1)n-1(+++…+xn)-(a1+a2+a3+…+x)n-------------(7分)
则
g′(x)=(k+1)n-1•nxn-1-n(a1+a2+a3+…+x)n-1令g'(x)=0得
x=---------------(8分)
当0≤x≤
时,
g′(x)=(k+1)n-1•nxn-1-n(a1+a2+a3+…+x)n-1≤
n(a1+a2+a3+…+x)n-1-
n(a1+a2+a3+…+x)n-1=0
故g(x)在
[0,]上递减,
类似地可证g(x)在
[,+∞)递增
∴当
x=时,g(x)的最小值为
g()------------(10分)
而
g()=
(k+1)n-1(++…++()n)-(a1+a2+…+ak+)n=
[kn(++…++(a1+a2+a3+…+ak)n)-(k+1)(a1+a2+…+ak)n]=
[kn(++…+)-k(a1+a2+…+ak)n]=
[kn-1(++…+)-(a1+a2+…+ak)n]由定理知:
kn-1(++…+)-(a1+a2+…+ak)n≥0,
故
g()≥0∵a
k+1∈[0,+∞),
∴
g(ak+1)≥g()≥0故
(k+1)n-1(+++…+)≥(a1+a2+a3+…+ak+1)n即:
≥()n---------------(14分)



 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.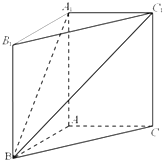 如图,在直三棱柱ABC-A1B1C1中,AC=AB=
如图,在直三棱柱ABC-A1B1C1中,AC=AB=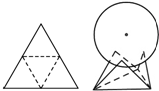 用一个边长为4的正三角形硬纸,沿各边中点连线垂直折起三个小三角形,做成一个蛋托,半径为1的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为
用一个边长为4的正三角形硬纸,沿各边中点连线垂直折起三个小三角形,做成一个蛋托,半径为1的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为