Question

【题目】对于函数，若在定义域内存在实数，满足，则称为“类函数”.

（1）已知函数，试判断是否为“类函数”？并说明理由；

（2）设是定义在上的“类函数”，求是实数的最小值；

（3）若 为其定义域上的“类函数”，求实数的取值范围.

Answer 1

【答案】（1）函数是“类函数”；（2）；（3）.

【解析】试题分析：(1) 由，得整理可得满足

(2) 由题存在实数满足，即方程在上有解.令分离参数可得，设求值域，可得

取最小值

(3) 由题即存在实数，满足，分， ， 三种情况讨论可得实数m的取值范围.

试题解析：（1）由，得：

所以

所以存在满足

所以函数是“类函数”，

（2）因为是定义在上的“类函数”，

所以存在实数满足，

即方程在上有解.

令

则，因为在上递增，在上递减

所以当或时， 取最小值

（3）由对恒成立，得

因为若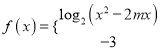 为其定义域上的“类函数”

所以存在实数，满足

①当时， ，所以，所以

因为函数（）是增函数，所以

②当时， ，所以，矛盾

③当时， ，所以，所以

因为函数 是减函数，所以

综上所述，实数的取值范围是

点睛:已知方程有根问题可转化为函数有零点问题，求参数常用的方法和思路有：

(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；

(2)分离参数法：先将参数分离，转化成函数的值域问题解决；

(3)数形结合法：先对解析式变形，在同一个平面直角坐标系中，画出函数的图像，然后数形结合求解.