
定义:若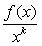 在
在 上为增函数,则称
上为增函数,则称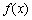 为“k次比增函数”,其中
为“k次比增函数”,其中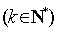 . 已知
. 已知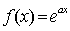 ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)若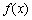 是“1次比增函数”,求实数a的取值范围;
是“1次比增函数”,求实数a的取值范围;
(2)当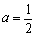 时,求函数
时,求函数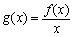 在
在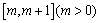 上的最小值;
上的最小值;
(3)求证:.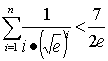
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
在平面直角坐标系中,记抛物线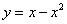 与x轴所围成的平面区域为
与x轴所围成的平面区域为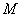 ,该抛物线与直线y=
,该抛物线与直线y=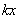 (k>0)所围成的平面区域为
(k>0)所围成的平面区域为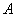 ,向区域
,向区域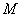 内随机抛掷一点
内随机抛掷一点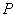 ,若点
,若点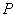 落在区域
落在区域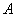 内的概率为
内的概率为 ,则k的值为
,则k的值为
查看答案和解析>>
科目:高中数学 来源: 题型:
为了迎接2010年广州亚运会,某大楼安装了5个彩灯,它们闪亮的顺序不固定.每个彩灯只能闪亮红、橙、黄、绿、蓝中的一种颜色,且这5个彩灯所闪亮的颜色各不相同,记这5个彩灯有序地各闪亮一次为一个闪烁.在每个闪烁中,每秒钟有且仅有一个彩灯闪亮,而相邻两个闪烁的时间、间隔均为5秒.如果要实现所有不同的闪烁,那么需要的时间至少是( )
A.1195秒 B.1190秒 C.1200秒 D.1205秒
查看答案和解析>>
科目:高中数学 来源: 题型:
实数m分别取什么数值时,复数z=(m2+5m+6)+(m2-2m-15)i
(1)与复数2-12i相等;
(2)与复数12+16i互为共轭复数;
(3)对应的点在x轴上方.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com