
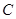 过点
过点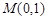 且与直线
且与直线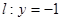 相切,设圆心
相切,设圆心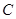 的轨迹为曲线
的轨迹为曲线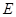 ,
,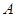 、
、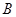 为曲线
为曲线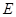 上的两点,点
上的两点,点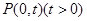 ,且满足
,且满足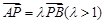 .
.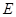 的方程;
的方程;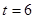 ,直线
,直线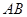 的斜率为
的斜率为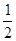 ,过
,过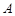 、
、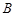 两点的圆
两点的圆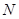 与抛物线在点
与抛物线在点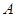 处有共同的切线,求圆
处有共同的切线,求圆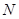 的方程;
的方程;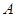 、
、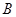 作曲线
作曲线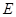 的切线,两条切线交于点
的切线,两条切线交于点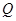 ,若点
,若点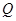 恰好在直线
恰好在直线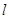 上,求证:
上,求证: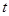 与
与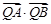 均为定值.
均为定值.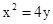 ;(2)
;(2)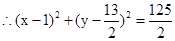 ;(3)0.
;(3)0.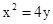 ;
; 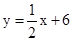 ,即x-2y+12=0,
,即x-2y+12=0,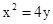 ,得点A、B、、的坐标是(6,9)或(-4,4),
,得点A、B、、的坐标是(6,9)或(-4,4),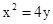 得
得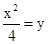 ,
,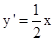 ,
,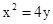 在点A处切线的斜率为
在点A处切线的斜率为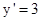 ,
, ,即x+3y-33=0…………①
,即x+3y-33=0…………①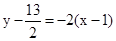 ,…………②
,…………②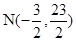
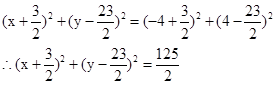 ,
,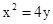 在点A处切线的斜率为
在点A处切线的斜率为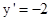 ,此时切线与AB垂直,所求圆为以AB为直径的圆,可求得圆为
,此时切线与AB垂直,所求圆为以AB为直径的圆,可求得圆为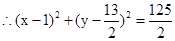 ,
, 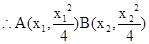 ,,Q(a,-1),过点A的切线方程为
,,Q(a,-1),过点A的切线方程为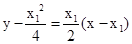 ,
,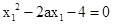 ,同理可得
,同理可得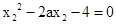 ,所以
,所以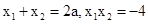 ,,
,,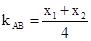 ,所以直线
,所以直线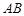 的方程为
的方程为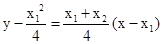 ,
,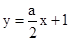 ,所以t=1,
,所以t=1, ,,所以
,,所以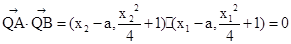


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源:不详 题型:解答题
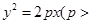

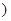 的对称轴上的定点
的对称轴上的定点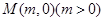 ,作直线
,作直线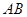 与抛物线相交于
与抛物线相交于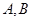 两点.
两点.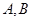 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;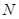 是定直线
是定直线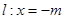 上的任一点,试探索三条直线
上的任一点,试探索三条直线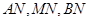 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
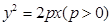 的焦点为F,过点F作直线
的焦点为F,过点F作直线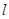 与抛物线交于A,B两点,抛物线的准线与
与抛物线交于A,B两点,抛物线的准线与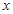 轴交于点C。
轴交于点C。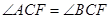 ;
;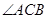 的最大值,并求
的最大值,并求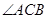 取得最大值时线段AB的长。
取得最大值时线段AB的长。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
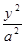 -
-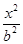 =1(a>0, b>0)有相同的焦点F,点B是两曲线的一个交点,且BF⊥y轴,若L为双曲线的一条渐近线,则L的倾斜角所在的区间可能是 ( )
=1(a>0, b>0)有相同的焦点F,点B是两曲线的一个交点,且BF⊥y轴,若L为双曲线的一条渐近线,则L的倾斜角所在的区间可能是 ( )A.(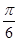 , ,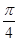 ) ) | B.(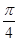 , ,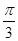 ) ) | C.(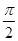 , ,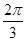 ) ) | D.(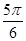 ,π) ,π) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com