
����Ŀ��ij���˾�����IJ������£�
��� ��Ŀ | 2014�� ��1-12�£� | 2015�� ��1-12�£� | 2016�� ��1-11�£� |
�ӵ��������� | 14463272 | 40125125 | 60331996 |
�ͷѣ�Ԫ�� | 214301962 | 581305364 | 653214963 |
ƽ��ÿ���ͷ� | 14.82 | 14.49 | |
ƽ��ÿ����� | 15 | 15 | |
ÿ�����ͺ� | 0.7 | 0.7 | 0.7 |
��Ͷ�������о���������ʱ���������˾�п�ʻ�������������ʻ�ʵļ��㹫ʽΪ![]() .
.
��1���ֱ����2014��2015��ù�˾�Ŀ�ʻ�ʵ�ֵ����ȷ��0.01%����
��2��2016��ù�˾��ǿ�����̹���������������������˿�ʻ�ʲ������ƽ��ÿ����̣������ֹ��11��30�գ���ʻ����2015��Ļ����Ͻ�����20���ٷֵ㣬��2016��ǰ11���µ�ƽ��ÿ���ͷѺ�ƽ��ÿ����̷ֱ�Ϊ���٣����ֱ�ȷ��0.01Ԫ��0.01���.
 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н�������ȷ�ĸ����ǣ� ����
����![]() ����
����![]() ����
����![]() �ǵ��������Σ�
�ǵ��������Σ�
����![]() ����
���� ![]() ����
����![]()
����������![]() ��
��![]() ���ߵij�Ҫ�����Ǵ���ʵ��
���ߵij�Ҫ�����Ǵ���ʵ��![]() ��ʹ
��ʹ![]()
�ܵȲ����е�ǰ![]() ���ʽ�dz�����Ϊ0�Ķ��κ�����
���ʽ�dz�����Ϊ0�Ķ��κ�����
A.0B.1C.2D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() .
.
��1����![]() ʱ��֤����
ʱ��֤����![]() ������
������![]() ������������
������������
��2����![]() ������
������![]() ������������˵�����ɣ�
������������˵�����ɣ�
��3������![]() �ĶԳ����ģ���˵������.
�ĶԳ����ģ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����
������![]() ��
��![]() ��������������
Ϊ��������������![]() �ϵ����е�ĺ����걣�ֲ��䣬����������Ϊԭ����
�ϵ����е�ĺ����걣�ֲ��䣬����������Ϊԭ����![]() ��õ�����
��õ�����![]() ��������ԭ��Ϊ���㣬
��������ԭ��Ϊ���㣬![]() ���������Ϊ���Ὠ��������ϵ��ֱ��
���������Ϊ���Ὠ��������ϵ��ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
��1��������![]() ��ֱ��
��ֱ��![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2����֪![]() ����ֱ��
����ֱ��![]() ������
������![]() ���ڲ�ͬ��
���ڲ�ͬ��![]() ��
��![]() ���㣬��
���㣬��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ʵ��
��ʵ��![]() ����
����![]() ��
��
��1��������![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��2��������ϵʽ![]() ��������
��������![]() �Ķ�����
�Ķ�����![]() ��
��
��3���ڣ�2���Ľ����У�������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
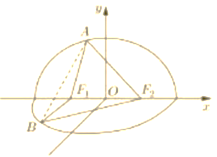
����Ŀ����֪��Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() ��������
��������![]() ����б��Ϊ
����б��Ϊ![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ��
��![]() ���㣨���е�
���㣨���е�![]() ��
��![]() ���Ϸ�����
���Ϸ�����![]() ���ܳ�Ϊ8��
���ܳ�Ϊ8��
��1������Բ![]() �ı����̣�
�ı����̣�
��2����ͼ����ƽ��![]() ��
��![]() ����������ʹ
����������ʹ![]() ���������
���������![]() ��ȷ���İ�ƽ�棬��
��ȷ���İ�ƽ�棬��![]() �������
�������![]() ����ȷ���İ�ƽ�滥�ഹֱ��
����ȷ���İ�ƽ�滥�ഹֱ��
����![]() ��������ֱ��
��������ֱ��![]() ��
��![]() ���ɽǵĴ�С��
���ɽǵĴ�С��
�����۵���![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ����
����![]() �Ĵ�С��
�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() Ϊ�����Σ�
������![]() ����
����![]() ��
��![]() ��
��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬![]() Ϊ�߶�
Ϊ�߶�![]() �ϵĶ���.
�ϵĶ���.
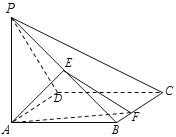
��1��ƽ��![]() ��ƽ��
��ƽ��![]() �Ƿ��ഹֱ�������ֱ����֤�����������ֱ����˵�����ɣ�
�Ƿ��ഹֱ�������ֱ����֤�����������ֱ����˵�����ɣ�
��2����![]() ��
��![]() Ϊ�߶�
Ϊ�߶�![]() �����ȷֵ㣬�������
�����ȷֵ㣬�������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �ֱ���˫����
�ֱ���˫����![]() �����ҽ��㣬��
�����ҽ��㣬��![]() б��Ϊ
б��Ϊ![]() ��ֱ��
��ֱ��![]() ��˫���ߵ�������֧�ֱ���
��˫���ߵ�������֧�ֱ���![]() ���㣬��
���㣬��![]() ����
����![]() ��ֱ��ֱ��
��ֱ��ֱ��![]() ��˫���ߵ�������֧�ֱ���
��˫���ߵ�������֧�ֱ���![]() ����.
����.
��1����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(2)���ı���![]() �������Сֵ
�������Сֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1������![]() �Ķ�����D�����ж�
�Ķ�����D�����ж�![]() ����ż�ԣ�
����ż�ԣ�
��2�������![]() ʱ��
ʱ��![]() ��ֵ����
��ֵ����![]() ����a��ֵ��
����a��ֵ��
��3���������m��![]() ���Ƿ����
���Ƿ����![]() ��ʹ��
��ʹ��![]() �������ڣ����t���������ڣ���˵�����ɣ�
�������ڣ����t���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com