
.函数 是
是 上的可导函数,
上的可导函数,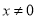 时,
时,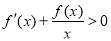 ,则函数
,则函数 的零点个数为( )
的零点个数为( )
A.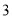 B.
B.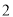 C.
C.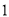 D.
D.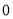
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源:2015届江西省高二下学期期末考试理科数学试卷(解析版) 题型:填空题
如图,在正方体 中,点
中,点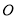 为线段
为线段 的中点。设点
的中点。设点 在线段
在线段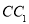 上,直线
上,直线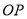 与平面
与平面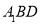 所成的角为
所成的角为 ,则
,则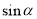 的取值范围是 。
的取值范围是 。

查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
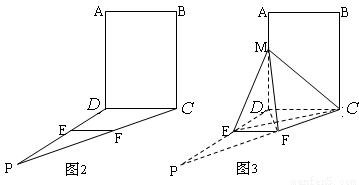
如图2,四边形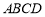 为矩形,
为矩形,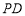 ⊥平面
⊥平面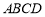 ,
,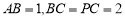 ,作如图3折叠,折痕
,作如图3折叠,折痕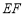
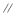
 ,其中点
,其中点 分别在线段
分别在线段 上,沿
上,沿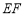 折叠后点
折叠后点 叠在线段
叠在线段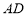 上的点记为
上的点记为 ,并且
,并且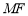 ⊥
⊥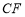 .(1)证明:
.(1)证明: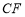 ⊥平面
⊥平面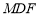 ;
;
(2)求三棱锥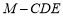 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试文科数学试卷(解析版) 题型:填空题
甲、乙两套设备生产的同类型产品共4800件,采用分层抽样的方法从中抽取一个容量为80的样本进行质量检测.若样本中有50件产品由甲设备生产,则乙设备生产的产品总数为 件.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
若函数f(x)= +2(a-1)x+2在区间
+2(a-1)x+2在区间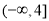 内递减,那么实数a的取值范围为( )
内递减,那么实数a的取值范围为( )
A.a≤-3 B.a≥-3 C.a≤5 D.a≥3
查看答案和解析>>
科目:高中数学 来源:2015届江西省上饶市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知函数f(x)=4cos2x﹣4 sinxcosx﹣2(x∈R).
sinxcosx﹣2(x∈R).
(1)求函数f(x)的单调递增区间;
(2)设△ABC的内角A,B,C对应边分别为a、b、c,且c=3,f(C)=﹣4,若向量 =(1,sinA)与向量
=(1,sinA)与向量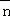 =(1,2sinB)共线,求a、b的值.
=(1,2sinB)共线,求a、b的值.
查看答案和解析>>
科目:高中数学 来源:2015届江西省上饶市高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知椭圆C: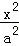 +
+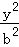 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是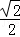 ,且点P(1,
,且点P(1,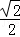 )在椭圆上.
)在椭圆上.
(1)求椭圆的方程;
(2)若过点D(0,2)的直线l与椭圆C交于不同的两点E,F,试求△OEF面积的取值范围(O为坐标原点).
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
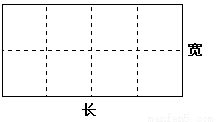
某水产养殖场拟造一个无盖的长方体水产养殖网箱,为了避免混养,箱中要安装一些筛网,其平面图如下,如果网箱四周网衣(图中实线部分)建造单价为每米56元,筛网(图中虚线部分)的建造单价为每米48元,网箱底面面积为160平方米,建造单价为每平方米50元,网衣及筛网的厚度忽略不计.
(1)把建造网箱的总造价y(元)表示为网箱的长x(米)的函数,并求出最低造价;
(2)若要求网箱的长不超过15米,宽不超过12米,则当网箱的长和宽各为多少米时,可使总造价最低?(结果精确到0.01米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com