
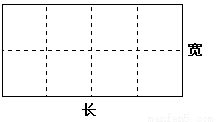
ijˮ����ֳ������һ���ǵij�����ˮ����ֳ���䣬Ϊ�˱������������Ҫ��װһЩɸ������ƽ��ͼ���£���������������£�ͼ��ʵ�߲��֣����쵥��Ϊÿ��56Ԫ��ɸ����ͼ�����߲��֣��Ľ��쵥��Ϊÿ��48Ԫ������������Ϊ160ƽ���ף����쵥��Ϊÿƽ����50Ԫ�����¼�ɸ���ĺ�Ⱥ��Բ���.
��1���ѽ�������������y��Ԫ����ʾΪ����ij�x���ף��ĺ���������������ۣ�
��2����Ҫ������ij�������15�ף���������12�ף�������ij��Ϳ���Ϊ������ʱ����ʹ�������ͣ��������ȷ��0.01�ף�
��1��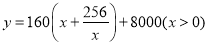 �����Ϊ13120Ԫ����2�����䳤Ϊ15m����Ϊ10.67mʱ����ʹ��������
�����Ϊ13120Ԫ����2�����䳤Ϊ15m����Ϊ10.67mʱ����ʹ��������
��������
�����������1����������������Ϊ�����������½����������ɸ�����������֮��. ����ij�x���� ����Ŀ�Ϊ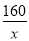 ������
������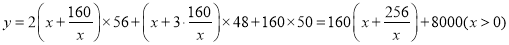 .��
.��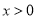 ʱ��
ʱ��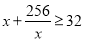 �����ҽ���
�����ҽ���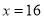 ʱȡ�Ⱥţ���ʱ
ʱȡ�Ⱥţ���ʱ ��2����Ϊ����ij�������15�ף���������12�ף����ԣ�1���еȺŲ�����.��ӵ������Ͽ�����ֵ. ��Ϊ
��2����Ϊ����ij�������15�ף���������12�ף����ԣ�1���еȺŲ�����.��ӵ������Ͽ�����ֵ. ��Ϊ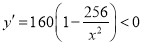 ������
������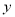 ��
��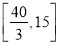 �ϵ����ݼ�����
�ϵ����ݼ�����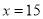 ʱ��y��С����ʱ��=
ʱ��y��С����ʱ��=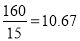 .
.
������Ŀ�Ϊ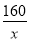 ��
��
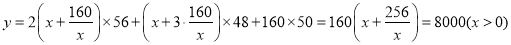 4��
4��
��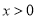 ʱ��
ʱ�� �����ҽ���
�����ҽ���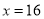 ʱȡ
ʱȡ
��ʱ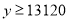
 ����ij�Ϊ16mʱ����������Ϊ13120Ԫ 8��
����ij�Ϊ16mʱ����������Ϊ13120Ԫ 8��
�������� 10��
10��
��ʱ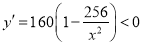 ��
��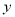 ��
��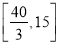 �ϵ����ݼ�����
�ϵ����ݼ�����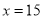 ʱ��y��С����ʱ��=
ʱ��y��С����ʱ��=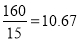 .
.
 ���䳤Ϊ15m����Ϊ10.67mʱ����ʹ�������� 16��
���䳤Ϊ15m����Ϊ10.67mʱ����ʹ�������� 16��
���㣺����Ӧ���⣬���ò���ʽ������������ֵ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�߶���ѧ����ĩ�����Ŀ���ѧ�Ծ��������棩 ���ͣ�ѡ����
������ ��
�� �ϵĿɵ�����,
�ϵĿɵ�����,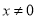 ʱ��
ʱ��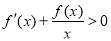 ������
������ ���������� ��
���������� ��
A��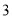 B��
B��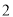 C��
C��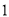 D��
D��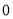
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�����и߶���ѧ����ĩ�����Ŀ���ѧ�Ծ��������棩 ���ͣ�ѡ����
Ҫ�õ�����y=f�䣨x����ͼ���轫����f��x��=sinx��cosx��x��R����ͼ������
A������ƽ��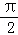 ����λ B������ƽ��
����λ B������ƽ��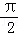 ����λ
����λ
C������ƽ�Ʀи���λ D������ƽ�Ʀи���λ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�߶���ѧ�����п���������ѧ�Ծ��������棩 ���ͣ������
���� ��
�� ��������������ʵ��
��������������ʵ��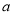 ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�߶���ѧ�����п���������ѧ�Ծ��������棩 ���ͣ������
��֪���� ����
���� ��
�� ����
����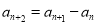 ����
����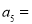
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�߶���ѧ�����п����Ŀ���ѧ�Ծ��������棩 ���ͣ������
��֪��ԲE�����ҽ���ֱ�F1��F2����F1��б��Ϊ2��ֱ�߽���ԲE��P��Q���㣬����PF1F2Ϊֱ�������Σ�����ԲE��������Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�߶���ѧ�����п����Ŀ���ѧ�Ծ��������棩 ���ͣ������
������ͼ��ʾ������ͼ��������Ľ��TΪ .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�����и���9�µ��п�����ѧ�Ծ��������棩 ���ͣ������
��Բ���ĵ���ֱ���߶������ֱ�����Բ������ı�����ֱ��Ϊ ��
��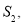 ����
����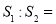
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ̩���н������߶���ѧ�����п���������ѧ�Ծ��������棩 ���ͣ������
��֪����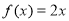 ��
��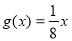 ����
����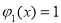 ����
���� ��
��
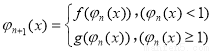 ����
���� ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com