
分析 (Ⅰ)由椭圆的两个焦点分分别为F1,F2,|F1F2|=2$\sqrt{3}$,长轴长为4,求出a,b,由此能求出椭圆C的方程.
(Ⅱ)设点P(x0,y0),则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=(-$\sqrt{3}-{x}_{0}$,0-y0)•($\sqrt{3}-{x}_{0},0-{y}_{0}$)=$\frac{3{{x}_{0}}^{2}}{4}-2$,由此能求出$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$的取值范围.
(Ⅲ)由M在直线l:x=4上,则点M(4,t),由A(-2,0),B(2,0),得AP:y=$\frac{t}{6}(x+2)$,BP:y=$\frac{t}{6}(x-2)$,从而求出P、Q的坐标,由此能求出直线PQ过定点(1,0).
解答 解:(Ⅰ)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点分分别为F1,F2,|F1F2|=2$\sqrt{3}$,长轴长为4,
∴$\left\{\begin{array}{l}{2c=2\sqrt{3}}\\{2a=4}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=1,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(Ⅱ)设点P(x0,y0),
∵P是椭圆C上任意一点,∴$\frac{{{x}_{0}}^{2}}{4}+{{y}_{0}}^{2}$=1,
∵|F1F2|=2$\sqrt{3}$,∴F${\;}_{1}(-\sqrt{3},0)$,F2($\sqrt{3},0$),
∴$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=(-$\sqrt{3}-{x}_{0}$,0-y0)•($\sqrt{3}-{x}_{0},0-{y}_{0}$)
=${{x}_{0}}^{2}-3+{{y}_{0}}^{2}$=${{x}_{0}}^{2}-3+1-\frac{{{x}_{0}}^{2}}{4}$=$\frac{3{{x}_{0}}^{2}}{4}-2$,
∵$0≤{{x}_{0}}^{2}≤4$,
∴$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$的取值范围是[-2,1].
(Ⅲ)∵M在直线l:x=4上,则点M(4,t),
∵A(-2,0),B(2,0),∴AP:y=$\frac{t}{6}(x+2)$,BP:y=$\frac{t}{6}(x-2)$,
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=\frac{t}{6}(x+2)}\end{array}\right.$,得P($\frac{18-2{t}^{2}}{{t}^{2}+9}$,$\frac{6t}{{t}^{2}+9}$),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=\frac{t}{6}(x-2)}\end{array}\right.$,得Q($\frac{2{t}^{2}-2}{{t}^{2}+1}$,-$\frac{2t}{{t}^{2}+1}$),
∴${k}_{PQ}=\frac{2t}{3-{t}^{2}}$,
∴PQ:y+$\frac{2t}{{t}^{2}+1}=\frac{2t}{3-{t}^{2}}(x-\frac{2{t}^{2}-2}{{t}^{2}+1})$,
y=$\frac{2t}{3-{t}^{2}}x-\frac{2t}{3-{t}^{2}}•\frac{2{t}^{2}-2}{{t}^{2}+1}-\frac{2t}{{t}^{2}+1}$,
y=$\frac{2t}{3-{t}^{2}}x-\frac{(2{t}^{2}-2)2t+2t(3-{t}^{2})}{({t}^{2}+1)(3-{t}^{2})}$,
y=$\frac{2t}{3-{t}^{2}}x-\frac{2t}{3-{t}^{2}}$,
∴PQ:y=$\frac{2t}{3-{t}^{2}}(x-1)$,
∴直线PQ过定点(1,0).
点评 本题考查椭圆方程的求法,考查向量的数量积的取值范围的求法,考查直线能否过定点的判断与求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
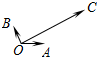 如图,平面内有三个向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,|$\overrightarrow{OC}|=2\sqrt{3}$,若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$(x,y∈R),则(x,y)=(4,2).
如图,平面内有三个向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,|$\overrightarrow{OC}|=2\sqrt{3}$,若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$(x,y∈R),则(x,y)=(4,2).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com