
分析 (1)讨论a,判断h′(x)的符号,得出h(x)的单调性;
(2)利用函数图象计算出a,根据导数判断g(x)的单调性,求出g(x)在(e-2,e)上的最大值即可得出m的范围.
解答 解:(1)由题意可知x>0,h′(x)=2x+2+$\frac{a}{x}$=$\frac{2{x}^{2}+2x+a}{x}$,
令m(x)=2x2+2x+a,则m(x)在(0,+∞)上单调递增,
∴m(x)>m(0)=a,
∴当a≥0时,m(x)>0,即h′(x)>0,∴h(x)在(0,+∞)上单调递增;
当a<0时,令m(x)=0得x=$\frac{\sqrt{1-2a}-1}{2}$,
∴当0<x<$\frac{\sqrt{1-2a}-1}{2}$时,m(x)<0,当x>$\frac{\sqrt{1-2a}-1}{2}$时,m(x)>0,
∴当0<x<$\frac{\sqrt{1-2a}-1}{2}$时,h′(x)<0,当x>$\frac{\sqrt{1-2a}-1}{2}$时,h′(x)>0,
∴h(x)在(0,$\frac{\sqrt{1-2a}-1}{2}$)上单调递减,在($\frac{\sqrt{1-2a}-1}{2}$,+∞)上单调递增.
综上,当a≥0时,h(x)在(0,+∞)上单调递增,
当a<0时,h(x)在(0,$\frac{\sqrt{1-2a}-1}{2}$)上单调递减,在($\frac{\sqrt{1-2a}-1}{2}$,+∞)上单调递增.
(2)g(x)=(x2-2x)lnx+ax2-x,
∵g(x)有且只有一个零点,∴(x2-2x)lnx=x-ax2只有一解,
即lnx=$\frac{x-a{x}^{2}}{{x}^{2}-2x}$有一解,
作出y=lnx与y=$\frac{x-a{x}^{2}}{{x}^{2}-2x}$=-a+$\frac{1-2a}{x-2}$的函数图象,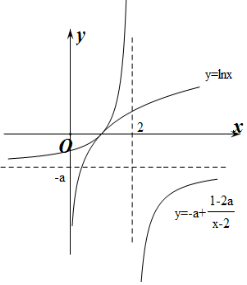
若1-2a>0即a$<\frac{1}{2}$时,两函数有两个交点,不符合题意,
当1-2a<0即a$>\frac{1}{2}$时,若两函数只有1个交点,则y=lnx与y=-a+$\frac{1-2a}{x-2}$有一条公共切线,
设切点为(x0,y0),则$\left\{\begin{array}{l}{\frac{1}{{x}_{0}}=-\frac{1-2a}{({x}_{0}-2)^{2}}}\\{ln{x}_{0}=-a+\frac{1-2a}{{x}_{0}-2}}\end{array}\right.$,解得x0=1,a=1.
∴g(x)=(x2-2x)lnx+x2-x,g′(x)=(2x-2)lnx+x-2+2x-1=(2x-2)lnx+3x-3=(x-1)(2lnx+3),
令g′(x)=0得x=1或x=e${\;}^{-\frac{3}{2}}$,
∴当0<x<e${\;}^{-\frac{3}{2}}$或x>1时,g′(x)>0,当e${\;}^{-\frac{3}{2}}$<x<1时,g′(x)<0,
∴g(x)在(0,e${\;}^{-\frac{3}{2}}$)上单调递增,在(e${\;}^{-\frac{3}{2}}$,1)上单调递减,在(1,+∞)上单调递增.
∵e-2<e${\;}^{-\frac{3}{2}}$<1<e,
∴g(x)在(e-2,e${\;}^{-\frac{3}{2}}$)上单调递增,在(e${\;}^{-\frac{3}{2}}$,1)上单调递减,在(1,e)上单调递增.
∵g(e${\;}^{-\frac{3}{2}}$)=-$\frac{1}{2}$e-3+2e${\;}^{-\frac{3}{2}}$,g(1)=0,
令m(x)=-$\frac{1}{2}$x2+2x=-$\frac{1}{2}$(x-2)2+2,则m(x)在(0,2)上单调递增,
∴m(e${\;}^{-\frac{3}{2}}$)>m(0)=0,即g(e${\;}^{-\frac{3}{2}}$)>0,∴g(e${\;}^{-\frac{3}{2}}$)>g(1),
∴当e-2<x<e时,g(x)≤-$\frac{1}{2}$e-3+2e${\;}^{-\frac{3}{2}}$.
∴m≥-$\frac{1}{2}$e-3+2e${\;}^{-\frac{3}{2}}$.
点评 本题考查了导数与函数单调性的关系,函数最值得计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -156 | B. | -128 | C. | -28 | D. | 128 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\overrightarrow a}{{|{\overrightarrow a}|}}+\frac{\overrightarrow b}{{|{\overrightarrow b}|}}$ | B. | $\frac{\overrightarrow a+\overrightarrow b}{{|{\overrightarrow a+\overrightarrow b}|}}$ | ||
| C. | $\frac{{|{\overrightarrow b}|\overrightarrow a-|{\overrightarrow a}|\overrightarrow b}}{{|{\overrightarrow a}|+|{\overrightarrow b}|}}$ | D. | $λ(\frac{\overrightarrow a}{{|{\overrightarrow a}|}}+\frac{\overrightarrow b}{{|{\overrightarrow b}|}})$,λ由$\overrightarrow{OM}$确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{23}{25}$ | B. | -$\frac{23}{25}$ | C. | $\frac{7}{8}$ | D. | -$\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 110 | B. | 216 | C. | 214 | D. | 218 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com