
| A. | -156 | B. | -128 | C. | -28 | D. | 128 |
分析 利用二项式展开式的通项公式,求出展开式中系数为有理数的项,
再计算系数为有理数的各项系数和.
解答 解:($\root{6}{2}$-$\frac{2}{x}$)7的展开式中,通项公式为
Tr+1=${C}_{7}^{r}$•${(\root{6}{2})}^{7-r}$•${(-\frac{2}{x})}^{r}$=(-1)r•${C}_{7}^{r}$•${2}^{\frac{7+5r}{6}}$•x-r;
令$\frac{7+5r}{6}$为整数,其中r=0,1,2,…,7;
由题意知,当r=1或r=7时,展开式中系数为有理数;
所以系数为有理数的各项系数之和为
-${C}_{7}^{1}$•22-${C}_{7}^{7}$•27=-28-128=-156.
故选:A.
点评 本题考查了二项式展开式的通项公式,以及项的系数为有理数的条件和应用问题,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {k|k≥$\frac{3}{4}$或k≤-4} | B. | {k|-4≤k≤$\frac{3}{4}$} | C. | {k|-$\frac{3}{4}$≤k<4} | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
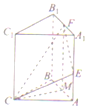 在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上
在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com