
| A. | $\frac{23}{25}$ | B. | -$\frac{23}{25}$ | C. | $\frac{7}{8}$ | D. | -$\frac{7}{8}$ |
分析 运用诱导公式得出cos($\frac{π}{8}$-α)=$sin(\frac{3π}{8}+α)$,再利用二倍角公式求出cos($\frac{3π}{4}$+2α)的值即可.
解答 解:∵cos($\frac{π}{8}$-α)=$sin[\frac{π}{2}-(\frac{π}{8}-α)]=sin(\frac{3π}{8}+α)=\frac{1}{5}$,
∴cos($\frac{3π}{4}$+2α)=$1-2si{n}^{2}(\frac{3π}{8}+α)=1-2×(\frac{1}{5})^{2}=\frac{23}{25}$.
故选:A.
点评 本题考查三角函数的化简求值,考查三角函数的诱导公式及运用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
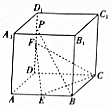 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的体积为$\frac{41\sqrt{41}}{6}π$.
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的体积为$\frac{41\sqrt{41}}{6}π$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
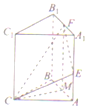 在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上
在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在(0,+∞)上是增函数 | B. | f(x)在(-∞,0)上是减函数 | ||
| C. | 当x=1时,f(x)取得极小值 | D. | f(0)+f(2)≥2f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 生二胎 | 不生二胎 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com