
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 Sn=2an-1,n=1时,a1=2a1-1,解得a1.n≥2时,an=Sn-Sn-1,化为:an=2an-1,利用等比数列的通项公式可得:an=2n-1.$\frac{{a}_{n}}{n}≤2$化为:2n-1≤2n,即2n≤4n.验证n=1,2,3,4时都成立.n≥5时,2n=(1+1)n,利用二项式定理展开即可得出.2n>4n.
解答 解:Sn=2an-1,n=1时,a1=2a1-1,解得a1=1.
n≥2时,an=Sn-Sn-1=2an-1-(2an-1-1),化为:an=2an-1,
∴数列{an}是等比数列,公比为2.
an=2n-1.
$\frac{{a}_{n}}{n}≤2$化为:2n-1≤2n,即2n≤4n.
n=1,2,3,4时都成立.
n≥5时,2n=(1+1)n=$1+{∁}_{n}^{1}$+${∁}_{n}^{2}$+…+${∁}_{n}^{n-2}$+${∁}_{n}^{n-1}$+${∁}_{n}^{n}$≥2($1+{∁}_{n}^{1}$+${∁}_{n}^{2}$)=n2+n+2,
下面证明:n2+n+2>4n,
作差:n2+n+2-4n=n2-3n+2=(n-1)(n-2)>0,
∴n2+n+2>4n,
则满足$\frac{{a}_{n}}{n}≤2$的最大正整数n的值为4.
故答案为:C.
点评 本题考查了数列递推关系、等比数列的通项公式、二项式定理的应用,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\overrightarrow a}{{|{\overrightarrow a}|}}+\frac{\overrightarrow b}{{|{\overrightarrow b}|}}$ | B. | $\frac{\overrightarrow a+\overrightarrow b}{{|{\overrightarrow a+\overrightarrow b}|}}$ | ||
| C. | $\frac{{|{\overrightarrow b}|\overrightarrow a-|{\overrightarrow a}|\overrightarrow b}}{{|{\overrightarrow a}|+|{\overrightarrow b}|}}$ | D. | $λ(\frac{\overrightarrow a}{{|{\overrightarrow a}|}}+\frac{\overrightarrow b}{{|{\overrightarrow b}|}})$,λ由$\overrightarrow{OM}$确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
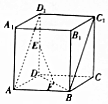 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{23}{25}$ | B. | -$\frac{23}{25}$ | C. | $\frac{7}{8}$ | D. | -$\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 1或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a100=-a,S100=2b-a | B. | a100=-b,S100=2b-a | ||
| C. | a100=-b,S100=b-a | D. | a100=-a,S100=b-a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com