
分析 (1)设P(x,y),则P到圆的切线长为$\sqrt{(x+2)^{2}+{y}^{2}-1}$,利用勾股定理列方程化简即可得出动点P的轨迹C的方程;
(2)当t=$\sqrt{3}$时,轨迹C的方程化为:$\frac{(x-1)^{2}}{\frac{5}{2}}-\frac{{y}^{2}}{5}=1$.可得曲线G的方程为$\frac{{x}^{2}}{\frac{5}{2}}-\frac{{y}^{2}}{5}=1$.可得曲线G的渐近线方程为y=$\sqrt{2}$x,y=-$\sqrt{2}$x.设Q(x0,y0),P1(m,$\sqrt{2}$m),P2(n,-$\sqrt{2}$n),$\frac{{y}_{0}-\sqrt{2}m}{{x}_{0}-m}=-\frac{\sqrt{2}}{2}$,$\frac{{y}_{0}+\sqrt{2}n}{{x}_{0}-n}$=$\frac{\sqrt{2}}{2}$.可得m,n.又y02=2x02-5,利用数量积运算性质即可得出;
(3)对曲线C得类型进行讨论,得出∠F1QF2的最大值,利用三角恒等变换列不等式解出t的范围.
解答 解:(1)圆(x+2)2+y2=1的圆心为M(-2,0),半径r=1,
设P(x,y),则P到圆的切线长为$\sqrt{(x+2)^{2}+{y}^{2}-1}$,
∴$\sqrt{(x+2)^{2}+{y}^{2}-1}$=t|x|,
∴(x+2)2+y2-1=t2x2,
整理得(1-t2)x2+y2+4x+3=0.
则动点P的轨迹C的方程为:(1-t2)x2+y2+4x+3=0.
(2)当t=$\sqrt{3}$时,轨迹C的方程为-2x2+4x+3+y2=0,即$\frac{(x-1)^{2}}{\frac{5}{2}}-\frac{{y}^{2}}{5}=1$.
∴曲线G的方程为$\frac{{x}^{2}}{\frac{5}{2}}-\frac{{y}^{2}}{5}=1$.
∴曲线G的渐近线方程为y=$\sqrt{2}$x,y=-$\sqrt{2}$x.
设Q(x0,y0),P1(m,$\sqrt{2}$m),P2(n,-$\sqrt{2}$n),
∴$\frac{{y}_{0}-\sqrt{2}m}{{x}_{0}-m}=-\frac{\sqrt{2}}{2}$,$\frac{{y}_{0}+\sqrt{2}n}{{x}_{0}-n}$=$\frac{\sqrt{2}}{2}$.
∴m=$\frac{2{y}_{0}+\sqrt{2}{x}_{0}}{3\sqrt{2}}$,n=$\frac{\sqrt{2}{x}_{0}-2{y}_{0}}{3\sqrt{2}}$,
∵$\frac{{{x}_{0}}^{2}}{\frac{5}{2}}-\frac{{{y}_{0}}^{2}}{5}=1$,∴y02=2x02-5,
∴$\overrightarrow{Q{P_1}}•\overrightarrow{Q{P_2}}$=(m-x0)(n-x0)+($\sqrt{2}$m-y0)(-$\sqrt{2}$n-y0)=(m-x0)(n-x0)-$\frac{\sqrt{2}}{2}$(x0-m)•$\frac{\sqrt{2}}{2}$(x0-n)
=$\frac{1}{2}$(m-x0)(n-x0),
=$\frac{1}{2}$•$\frac{2{y}_{0}-2\sqrt{2}{x}_{0}}{3\sqrt{2}}$•$\frac{-2\sqrt{2}{x}_{0}-2{y}_{0}}{3\sqrt{2}}$=$\frac{2{{x}_{0}}^{2}-{{y}_{0}}^{2}}{9}$=$\frac{5}{9}$.
(3)曲线C的方程可化为(1-t2)(x+$\frac{2}{1-{t}^{2}}$)2+y2=$\frac{4}{1-{t}^{2}}$-3,
当0<t<1时,曲线C为焦点在x轴上的椭圆,椭圆标准方程为$\frac{(x+\frac{2}{1-{t}^{2}})^{2}}{\frac{3{t}^{2}+1}{(1-{t}^{2})^{2}}}$+$\frac{{y}^{2}}{\frac{3{t}^{2}+1}{1-{t}^{2}}}$=1
∴当Q为短轴端点时,∠F1QF2取得最大值,设∠F1QF2的最大值为α,则tan2$\frac{α}{2}$=$\frac{{c}^{2}}{{b}^{2}}$=$\frac{\frac{3{t}^{2}+1}{(1-{t}^{2})^{2}}-\frac{3{t}^{2}+1}{1-{t}^{2}}}{\frac{3{t}^{2}+1}{1-{t}^{2}}}$=$\frac{{t}^{2}}{1-{t}^{2}}$,
∴cosα=$\frac{1-ta{n}^{2}\frac{α}{2}}{1+ta{n}^{2}\frac{α}{2}}$=1-2t2,
若曲线C上不存在点Q,使∠F1QF2=θ,则θ>α,
∴cosθ<1-2t2,解得0<t<$\sqrt{\frac{1-cosθ}{2}}$.
当t>1时,曲线C为焦点在x轴的双曲线,∴0<∠F1QF2≤π,
∴当0<θ<π时,曲线C上始终存在的Q使得∠F1QF2=θ.
综上,当0<t<$\sqrt{\frac{1-cosθ}{2}}$时,曲线C上不存在点Q,使∠F1QF2=θ.
点评 本题考查了参数方程化为普通方程、直线与圆的位置关系、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
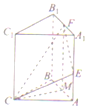 在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上
在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “a>b”是“a2>b2”的充分不必要条件 | |
| B. | 命题“?x0∈R,$x_0^2+1<0$”的否定是“?x∈R,x2+1>0” | |
| C. | 关于x的方程x2+(a+1)x+a-2=0的两实根异号的充要条件是a<1 | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在(0,+∞)上是增函数 | B. | f(x)在(-∞,0)上是减函数 | ||
| C. | 当x=1时,f(x)取得极小值 | D. | f(0)+f(2)≥2f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
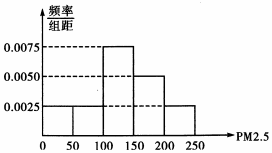 PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级
PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级| PM2.5 | [0,100) | [100,150) | [150,200) | [200,250] |
| 等级 | 一级 | 二级 | 三级 | 四级 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 92 | 81 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | 5 | 2 | 7 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com