Question

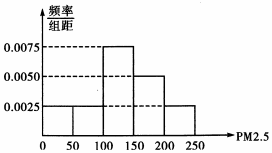
19．PM2.5是衡量空气污染程度的一个指标，为了了解某市空气质量情况，从去年每天的PM2.5值的数据中随机抽取40天的数据，其频率分布直方图如图所示．现将PM2.5的值划分为如下等级

PM2.5	[0，100）	[100，150）	[150，200）	[200，250]
等级	一级	二级	三级	四级

用频率估计概率．
（1）估计该市在下一年的360天中空气质量为一级天气的天数；
（2）在样本中，按照分层抽样的方法抽取8天的PM2.5值的数据，再从这8个数据中随机抽取5个，求一级、二级、三级、四级天气都有的概率；
（3）如果该市对环境进行治理，治理后经统计，每天PM2.5值X近似满足X～N（115，75²），则治理后的PM2.5值的均值比治理前大约下降了多少？

Answer 1

分析 （1）该市在下一年的360天中空气质量为一级天气的概率为0.125+0.125=0.25，即可估计该市在下一年的360天中空气质量为一级天气的天数；
（2）按照分层抽样的方法从一级、二级、三级、四级的PM2.5值的数据的比值为：50：75：50：25=2：3：2：1，
，确定基本事件的个数，即可得出结论；
（3）求出该市维持现状不变，该市PM2.5值，治理后的PM2.5值的均值即可得出结论．

解答 解：（1）由题意，该市在下一年的360天中空气质量为一级天气的概率为0.125+0.125=0.25，天数为90天；
（2）按照分层抽样的方法从一级、二级、三级、四级的PM2.5值的数据的比值为：50：75：50：25=2：3：2：1，
从这8个数据中随机抽取5个，共有${C}_{8}^{5}$=56种，一级、二级、三级、四级天气都有，有3种情况，一级天气2个，其余1个；二级天气2个，其余1个；三级天气2个，其余1个；
共有C₂²C₃²C₂¹C₁¹+C₂¹C₃²C₂¹C₁¹+C₂²C₃³C₂¹C₁¹=24种，故概率为$\frac{24}{56}$=$\frac{3}{7}$；
（3）如果该市维持现状不变，则该市PM2.5值约为E（Y）=25×0.125+75×0.125+125×0.375+175×0.25+225×0.125=131.25，治理后的PM2.5值的均值E（X）=115，
∴治理后的PM2.5值的均值比治理前大约下降了16.25．

点评 本题考查利用数学知识解决实际问题，考查概率的计算，考查学生的计算能力，属于中档题．