
| A. | 1 | B. | 2 | C. | 3 | D. | 1或3 |
分析 结合正弦函数的图象和性质可得|x1-x2|min=2,得φ的值
解答 解:将函数f(x)=2sin(πx)的图象向左平移φ(0<φ<4)个单位,得到函数y=g(x)=2sin(πx+φπ)的图象,
故f(x)的最大值为2,最小值为-2,g(x)的最大值为2,最小值为-2.
若实数x1,x2满足|f(x1)-g(x2)|=4,且|x1-x2|=2,两个函数的最大值与最小值的差为2,有|x1-x2|min=2.
不妨假设f(x1)=2,g(x2)=-2,则 πx1=2kπ+$\frac{π}{2}$,πx2+πφ=2nπ-$\frac{π}{2}$,k、n∈Z,
即x1=2k+$\frac{1}{2}$,x2=2n-$\frac{1}{2}$-φ,此时,有|x1-x2|min=2=|2k-2n+1+φ|=1+φ,或|x1-x2|min=2=|2k-2n+1+φ|=-2+1+φ,
∴φ=1 或φ=3,
故选:D.
点评 本题考查三角函数的图象平移,函数的最值以及函数的周期的应用,考查分析问题解决问题的能力,是好题,题目新颖,有一定难度,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{10}$ | B. | -$\frac{π}{5}$ | C. | $\frac{π}{10}$ | D. | $\frac{π}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
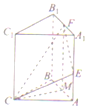 在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上
在三棱柱ABC-A1B1C1中,已知侧按AA1⊥底面ABC,且四边形AA1B1B是边长为2的正方形,CA=CB,点M为棱AB的中点,点E,F分别在按AA1,A1B1上查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “a>b”是“a2>b2”的充分不必要条件 | |
| B. | 命题“?x0∈R,$x_0^2+1<0$”的否定是“?x∈R,x2+1>0” | |
| C. | 关于x的方程x2+(a+1)x+a-2=0的两实根异号的充要条件是a<1 | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
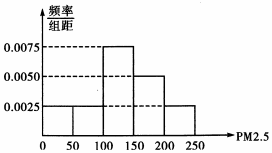 PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级
PM2.5是衡量空气污染程度的一个指标,为了了解某市空气质量情况,从去年每天的PM2.5值的数据中随机抽取40天的数据,其频率分布直方图如图所示.现将PM2.5的值划分为如下等级| PM2.5 | [0,100) | [100,150) | [150,200) | [200,250] |
| 等级 | 一级 | 二级 | 三级 | 四级 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com